y = 4x - x² - Квадратичная функция, график - парабола, ветви направлены вниз ( a = -1). Максимальное значение принимает в вершине, минимальное значение не имеет, снизу не ограничена.
a) Координаты вершины параболы
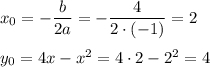
x₀=2 ∈ [0; 3] ⇒ x₀=2 - точка максимума функции попадает в заданный интервал, наибольшее значение функции y₀ = 4.
Значения функции на границах интервала
x = 0; y = 4·0 - 0² = 0
x = 3; y = 4·3 - 3² = 3
Наименьшее значение y = 0 при x = 0.
б) x∈(-∞; 2] - функция возрастает
x∈[2; +∞) - функция убывает
в) 4x - x² < 0 ⇔ x (4 - x) < 0
Метод интервалов : x₁ = 0; x₂ = 4
------------ (0) +++++++++ (4) -----------> x
x∈(-∞; 0) ∪ (4; +∞)
Пусть груш было -х,тогда яблок было 4-х,уменьшили яблоки4-х/2,4-х/2+x+4-x=5 4-x+2x+8-2x=10 -x=-2 x=2 кг-груши,4-2=2кг-яблоки