(см. объяснение)
Объяснение:
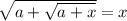
Если я правильно понял, то нужно решить уравнение при каждом значении параметра.
Возведем обе части уравнения в квадрат на условии, что 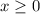 .
.
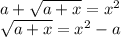
Возведем обе части уравнения в квадрат, добавив условие 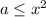 .
.
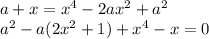
Решаем через дискриминант:
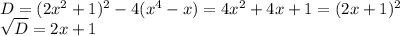
Найдем корни:

Итого исходному уравнению равносильно:
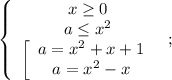
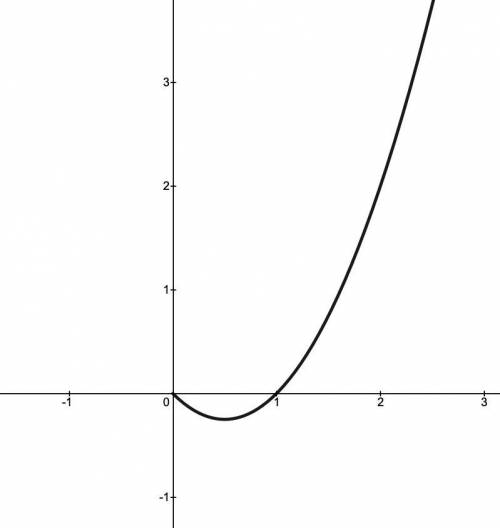
Строим все в координатах (x; a):
(см. прикрепленный файл)
Итого:
При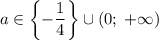 исходное уравнение имеет единственное решение.При
исходное уравнение имеет единственное решение.При ![a\in\left(-\dfrac{1}{4};\;0\right]](/tpl/images/2008/8379/66efc.png) исходное уравнение имеет ровно два различных решения.При
исходное уравнение имеет ровно два различных решения.При 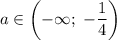 исходное уравнение не имеет решений.
исходное уравнение не имеет решений.Задание выполнено!
Доказательство:
Дана последовательность
Допустим, что эта последовательность арифметическая прогрессия, тогда
при n = 1 получаем
при n = 2
и
а₂ = -2 - а₁ = -2 + 2 = 0
Таким образом разность арифметической прогрессии
d = a₂ - a₁ = 0 + 2 = 2
По известной формуле найдем n-й член арифметической прогрессии
Известно, что сумма n членов арифметической прогрессии
Докажем, что выражение (2) тождественно выражению (1) при
a₁ = -2 и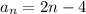 , подставив в (2)
, подставив в (2)
Тождество доказано.
Следовательно, последовательность, определённая суммой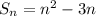 является арифметической прогрессией.
является арифметической прогрессией.