Для нахождения решения корней x2 - 6x = 16 полного квадратного уравнения мы начнем с того, что перенесем 16 в левую часть уравнения:
x2 - 6x - 16 = 0.
Для решения уравнения будем использовать формулы для поиска дискриминанта и корней уравнения через дискриминант.
D = b2 - 4ac = (-6)2 - 4 * 1 * (-16) = 36 + 64 = 100;
Корни уравнения мы вычислим по следующим формулам:
x1 = (-b + √D)/2a = (6 + √100)/2 * 1 = (6 + 10)/2 = 16/2 = 8;
x2 = (-b - √D)/2a = (6 - √100)/2 * 1 = (6 - 10)/2 = -4/2 = -2.
ответ: x = 8; x = -2.
Объяснение:
В решении.
Объяснение:
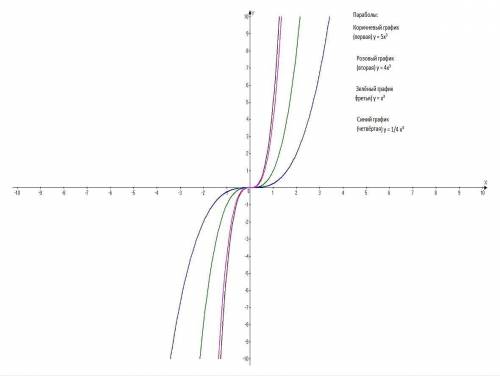
Построить в одной системе координат графики функций:
у = х³; у = 5х³; у = х³/4; у = 4х³.
Все графики - кубические параболы с вершиной в начале координат (0; 0). у = х³ - классическая парабола, остальные, в зависимости от коэффициента перед х³ "уже" или "шире" её.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
1) у = х³;
Таблица:
х -2 -1 0 1 2
у -8 -1 0 1 8
2) у = 5х³;
Таблица:
х -2 -1 0 1 2
у -40 -5 0 5 40
3) у = 1/4 х³ = х³/4;
Таблица:
х -3 -2 -1 0 1 2 3
у -6,75 -2 -0,25 0 0,25 2 6,75
4) у = 4х³;
Таблица:
х -2 -1 0 1 2
у -32 -4 0 4 32
Объяснение:
а) у=3×0-9 у=-9;
у=3×1,5-9 у=-4,5;
б) 3=3х-9
х=2
0=3х-9
х=3
6=3х-9
х=5