неверно
Объяснение:
в неравенстах, во-первых, нельзя домножать обе части неравенства на переменную, мы не знаем, какое там число. если бы было отрицательное, то мы бы меняли знак неравенства.
А еще в ходе решения, там почему-то поменялся знак у 2x и 8, хотя 8 была слева и должна остаться с плюсом.
И -28 - дискриминант квадратного уравнения, его надо использовать для получения корней уравнения, т.к корни уравнения - решения неравенств
решим неравенство правильно:
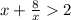
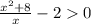
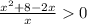
приравняем числитель и знаменатель к нулю
x²-2x+8=0; D=(-2)²-4*1*8=4-32=-28 - нет действительных корней
x=0
отметим точку на интервале и определим знак, для этого возьмем, например, точку 100 (см рис)
100+8/100>2
100+0,08>2
100,08>2 - знак +
и точку -1:
-1+8/-1>2
-1-8>2
-9>2 - знак -
знак неравенства >, значит выбираем интервал с плюсом
ответ: x ∈ (0; +∞)

Объяснение:
Выразим переменные х и у из уравнений:
1) у + 7 * х = 3;
Выразим переменную у через х.
Перенесем все значения кроме у на противоположную сторону. То есть получаем:
y = 3 - 7 * x;
Выразим переменную х через у.
y + 7 * x = 3;
7 * x = 3 - y;
x = (3 - y)/7;
2) 6 * х – 2 * у = -4;
{ 6 * x = 2 * y - 4;
-2 * y = -4 - 6 * x;
{ 3 * x = y - 2;
2 * y = 4 + 6 * x;
{ x = (y - 2)/3;
y = 2 + 3 * x;
3) х – у = -1;
{ x = -1 + y;
-y = -1 - x;
{ x = y - 1;
y = 1 + x;
4) х + 1,5 * у = 0,5;
{ x = 0.5 - 1.5 * y;
1.5 * y = 0.5 - x;
{ x = 0.5 - 1.5 * y;
y = (0.5 - x)/1.5.
y=x^3+6x^2+9x+4
y’=3x^2+12x+9
y’=0
3x^2+12x+9=0
x^2+4x+3=0
D=b^2-4ac=4
X1=-1
X2=-3
Методом интервалов определяем, что функция возрастает от –∞ до -3 и от -1 до +∞
Функция убывает от -3 до -1
При x=-1 y=0
При x=-3 y=4