Взаимно обратные функции Задание 1
Вопрос:
Найдите область определения и область значения функции, обратной данной у = 7х - 5.
Выберите несколько из 6 вариантов ответа:
1) E(y) = (-5;7) 2) D(y) = (-5;+∞)
3) E(y) = (-∞;+∞) 4) D(y) = (-7;+∞)
5) E(y) = (-∞;5) 6) D(y) = (-∞;+∞)
Задание 2
Вопрос:
Укажите номер рисунка, на котором изображён график обратной функции к функции у = х2, при х ∈ [0;+∞).
Изображение:
Запишите число:
Задание 3
Вопрос:
Укажите, какие из перечисленных функций являются обратимыми.
Выберите несколько из 4 вариантов ответа:
1) у = 5х + 2 2) у = х5
3) у = х2 4) у = х3 + 1
Задание 4
Вопрос:
Какое значение принимает обратная функция при х = 6 к функции у = 2х - 4.
Запишите число:
Задание 5
Вопрос:
Укажите истинные утверждения.
Если g(x) - функция, обратная к функции f(x), то и f(x) - функция, обратная к g(x), при этом ...
Выберите несколько из 4 вариантов ответа:
1) область определения обратной функции совпадает со множеством значений исходной функции
2) область определения обратной функции совпадает с областью определения исходной функции
3) множество значений обратной функции совпадает со множеством значений исходной функции
4) множество значений обратной функции совпадает с областью определения исходной функции
Задание 6
Вопрос:
Является ли монотонная функция обратимой?
Выберите один из 2 вариантов ответа:
1) не является 2) является
Задание 7
Вопрос:
Найдите область значений функции, обратной для f(x) = 4 - 3x
Выберите один из 5 вариантов ответа:
1) [-4;-3] 2) (0;+∞)
3) [3;4] 4) (-∞;+∞)
5) (-∞;4)
Задание 8
Вопрос:
Найдите функцию, обратную к функции у = 5х + 2
Выберите один из 4 вариантов ответа:
1) у = (х - 2)2 2) у = 0,5 (х - 2)
3) у = 0,2 (2 + х) 4) у = 0,2 (х - 2)
Задание 9
Вопрос:
Сопоставьте функции и обратные к ним.
Укажите соответствие для всех 3 вариантов ответа:
1) 2) 3)
__ у = 2х __ у = 3х – 5 __ у = х3
Задание 10
Вопрос:
Как называют функцию y = f(х), если она принимает каждое своё значение
только при одном значении х?
Запишите ответ:
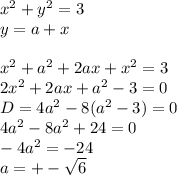
а)sin 5п/4=sin(π-π/4)=sin π/4=√2/2
б)tg 7п/6=tg(π+π/6)=tg π/6=√3/3
в)cos п/6 - ctg π/4=√3/2-1г)tg 3п/4 x cos 3п/4+сtg(-п/6) х sin п/6=sin 3π/4/cos 3π/4*cos 3π/4-cosπ/6/sinπ/6*sinπ/6=sin 3π/4-cos π/6=sin(π-π/4)-cosπ/6=sinπ/4-cosπ/6=√2/2-√3/2
д)sin 510-sin270 ctg270=sin (2π+π-30)-sin 270*cos270/sin270=sin30-cos(2π-90)=1/2-1=-0.5
2)Упростите выражение
сos^2 - sin^2t/tg(-t)ctgt=cos²t-sin²t/(-tg t)*ctg t=cos²t+sin²t=1
3)Решите уравнение:
a)sint=1/2
t=x = (-1)^k П/6 + Пk, k∈Z;
б)sin(п/2 + t)=- корень из 3/2
cos t=-√3/2
t=+-5π/6+2πk, k∈Z
4)Известно,что ctg(t-п)=-3/4 и п/2 п/2<t<п
ctg(-(π-t))=-ctg(π-t)=ctg t
ctg t=cos t/sin t=-3/4
4cost=-3sint
4cost=-3√(1-cos²t)
16cos²t=9(1-cos²t)
16cos²t=9-9cos²t
25cos²t=9
cos²t=9/25
cost=+-√(9/25)=+-3/5, cost<0 (t∈(π/2; π)
cost=-3/5=-0.6
sin t=cos t/ctg t=-0.6/(-3/4)=0.2*4=0.8
Найдите:
a)cos(3п/2 - t)=-sint=-0.8
б)cos(п + t)=-cost=-(-0.6)=0.6
5)Расположите в порядке возростания:
a=cos6
b=cos7
c=sin6=sin (π/2-(π/2-6))=cos (90-6)=cos 84
d=sin 4=sin (π/2-(π/2-4))=cos (90-4)=cos 86
Поскольку cos убывает на промежутке [0; π/2], то
cos 86<cos 84<cos7<cos6
d<c<b<a