Как представить выражение в виде произведения? а)х^3 -ху ^2 + 3у^2 - 3х^2 б) 8m^4-m^7

👇

Увидеть ответ

Ответ:

лолер2

02.01.2021

а)х^3 -ху ^2 + 3у^2 - 3х^2=x(x^2-y^2)-3(x^2-y^2)=(x-y)(x+y)(x-3)

б) 8m^4-m^7=m^4(8-m^3)=m^4(2-m)(4+2m+m^2)

4,8(89 оценок)

Ответ:

eruder

02.01.2021

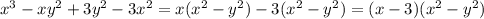
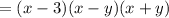
1) x^3-xy^2+3y^2-3x^2=x(x^2-y^2)-3(x^2-y^2)=(x-3)(x^2-y^2) =(x-3) (x-y) (x+y)

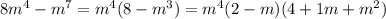
2) 8m^4-m^7=m^4(8-m^3)=m^4(2-m)(4+1m+m^2)

4,5(37 оценок)

Открыть все ответы

Ответ:

daniilzagora

02.01.2021

1) За 1017 взвешиваний Мистер Фокс сможет гарантированно узнать суммарный вес всех монет.

Он, к примеру, сначала взвесит 1014 "не пересекающихся" пар монет. И узнает их суммарный вес.

Останется еще 3 монеты (по причине того, что 2031 - 1014 · 2 = 3). Первая будет взвешена по очереди со второй и с третьей, а дальше на весах появятся вторая и третья монета.

Результатом таких взвешиваний будут три числа. Если мы их сложим, то получим удвоенный вес первой, второй и третьей монет. Если разделим на два, то получим вес всех трех оставшихся монет.

И прибавим его к весу взвешенных ранее 1014 пар монет. Получим суммарный вес всех монет.

2) Меньше, чем за 1017 взвешиваний, в общем случае суммарный вес монет не удастся узнать.

Почему? Очевидно, что при взвешиваниях каждая монета должна побывать на весах. Поэтому взвешиваний должно быть уже не меньше 1016 (2031 : 2 = 1015 пар монет, и 1 в остатке дает 1016-ое взвешивание).

Несложно понять, что если нам удалось за 1016 (или меньше) взвешиваний узнать суммарный вес монет, то: 1) все монеты побывали на весах; 2) ровно одна монета (обозначим ее буквой М) побывала на весах два раза, во второй раз - с монетой Л, образовавшейся в результате остатка при делении на 2 числа 2031.

Суммарный вес всех монет, кроме М нам известен. Следовательно, задача решится, если мы найдем Л. А чтобы найти Л, нужно найти М. Но М как из первого взвешивания, так и из второго найти нельзя.

Можно сказать, что получается что-то наподобие системы из двух линейных уравнений с тремя неизвестными (X + M = a, M + L = b).

Таким образом, за 1016 (и меньше) взвешиваний узнать суммарный вес всех монет не удастся. А за 1017 - уже получится.

4,4(50 оценок)

Ответ:

whatareyoudoing

02.01.2021

Сын мог бы выполнить один всю работу за 60 дней, а отец за 15 дней

Объяснение:

Весь объём работы принимаем за 1 (единицу)

Пусть сын один может выполнить всю работу за х дней, а отец за у дней. Планировалось, что работая вместе, отец и сын смогут выполнить всю работу за 12 дней, значит, за 1 день они сделают 1/12 работы. Составим первое уравнение:

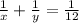
$\frac{1}{x}+\frac{1}{y}=\frac{1}{12}$

Сын работал 8 дней и за 8 дней сделал 8/х часть работы. Отец работал 8+5 =13 дней и за 13 дней сделал 13/у часть работы. Фактически вместе они выполнили весь объём работы = 1. Составляем второе уравнение:

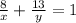
$\frac{8}{x}+\frac{13}{y}=1$

Решаем систему уравнений:

$\left \{ {{\frac{1}{x}+\frac{1}{y}=\frac{1}{12} } \atop {\frac{8}{x}+\frac{13}{y}=1}} \right.=\left \{ {{\frac{1}{x}=\frac{1}{12}-\frac{1}{y}} \atop {\frac{8}{x}+\frac{13}{y}=1}} \right.=\left \{ {{\frac{1}{x}=\frac{y-12}{12y} } \atop {\frac{8}{x}+\frac{13}{y} =1}} \right.=\frac{8(y-12)}{12y}+\frac{13}{y}=1\\\\\\\frac{2(y-12)}{3y}+\frac{39}{3y}=1\;|*3y\neq0\\\\2y-24+39=3y\\3y-2y=15\\y=15\\\\\frac{1}{x}=\frac{15-12}{15*12}\\\\\frac{1}{x}=\frac{3}{180}\\\\\frac{1}{x}=\frac{1}{60}\\\\x=60$