1) х + (2х + 0,5) = х + 2х + 0,5 = 3х + 0,5.
2) 3х - (х - 2) = 3х - х + 2 = 2х + 2.
3) 4а - (а + 6) = 4а - а - 6 = 3а - 6.
4) 6b + (10 - 4.5b) = 6b + 10 - 4.5b = 1.5b + 10.
Объяснение:
Упростим выражения.
1) х + (2х + 0,5) = х + 2х + 0,5 = 3х + 0,5.
2) 3х - (х - 2) = 3х - х + 2 = 2х + 2.
3) 4а - (а + 6) = 4а - а - 6 = 3а - 6.
4) 6b + (10 - 4.5b) = 6b + 10 - 4.5b = 1.5b + 10.
Для того, чтобы упростить данное выражение, мы в первую очередь раскрыли скобки. Если перед скобками стоит знак минус, то при раскрытии скобок мы меняем знаки членов в скобках на противоположные. Затем мы сгруппировали члены, которые содержат неизвестное и свободные члены.
а) n-ый член геометрической прогрессии ищется по формуле:
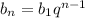
Тогда пятый член этой прогрессии равен:

б) Аналогично по формуле n-го члена геом. прогрессии вычисляем девятый член прогрессии:
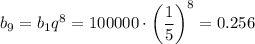
в) Сумма первых n членов геометрической прогрессии ищется по следующей формуле:
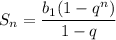
Тогда сумма первых восьми членов этой прогрессии равна:

г) Аналогично с в) по формуле суммы n первых членов геометрической прогрессии вычисляем сумму первых пяти членов этой прогрессии:
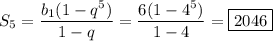
д) Предполагается, что нужно найти сумму бесконечно убывающей геометрической прогрессии:

Тогда
А) -36; - 12; -4;
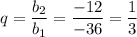
Сумма бесконечно уб. г.п. 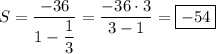
Б) 
Сумма бесконечно убывающей геометрической прогрессии:
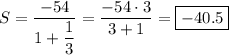
e) используя n-ый член геометрической прогрессии, рассмотрим пятый член этой прогрессии:
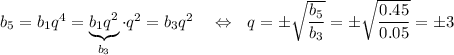
Так как по условию q>0, то q=3
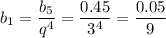
Сумма первых восьми членов этой прогрессии равна:

{5х-5у\4=5\2
{6х+3у\2= -15
Избавимся в каждом уравнении от знаменателя:
{5x*4-5y=5*2 {20x-5y=10
{6x*2+3y=-15*2 {12x+3y=-30
Из первого уравнения выразим у:
-5y=10-20x
y=(20x-10)/5=4x-2
Подставим во второе:
12x+3(4x-2)=-30
12x+12x-6=-30
24x=-24
x=-1
Найдём у:
у=4х-2=4*(-1)-2=-4-2=-6
ответ: (-1;-6)