Дано:
1 катет = х см
2 катет = (х+1) см
гипотенуза = 29 см
Теорема Пифагора: В прямоугольном треугольнике, квадрат гипотенузы равен сумме квадратов катетов c²=a²+b²
29²=x²+(x+1)²
x²+x²+2x+1=841
2x²+2x-840=0 | 2
x²+x-420=0
D=1²-4*1*(-420)
D=1681 √1681=41
x₁=(-1+41)/2=20
x₂=(-1-41)/2=-21 - сторонний корень, не соответствует условию
Получено 2 значения х, из них соответсвует условию только положительное значение х=20, потому, что длина не может быть отрицательным числом.
х=20 см
х+1=21 см
Проверка: 29²=20²+21²
841=400+441
841=841
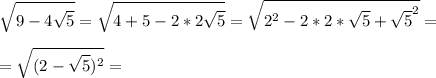
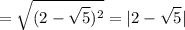
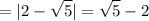
3x^2=10-29x (переносим всё в левую часть и получаем квадратное уравнение)
3x^2+29x-10=0
а=3, b=29, с=-10 (это коэфициенты)
D=b^2-4ac (формула дискриминанта)
D=29^2-4*3*(-10)= 961 (находим дискриминант)
D>0, 2 корня
х=-b+-√D/2a (это формула для нахождения корней)
x1=-29- √961/2*3=-10 (первый корень)
x2=-29+ √961/2*3=1/3 (второй корень)
ответ: -10; 1/3