Легко запомнить. Чтобы выделить полный квадрат (квадрат двучлена) из квадратного трёхчлена, надо разделить пополам коэффициент перед "х" и записать это число в скобку, которая будет возведена в квадрат ( ), а затем вычесть квадрат этой половины, а далее приписать свободный член q. Это правило годиться, если коэффициент при равен 1. Если этот коэффициент не равен 1, то предварительно вынести его за скобку и выделять полный квадрат из выражения, записанного в скобке.
Область допустимых значений (ОДЗ): x >= -4. x - 4*V(x + 4) - 1 < 0 ( V - корень квадратный). x - 1 < 4*V(x + 4) Правая часть неравенства <= 0 для всех х из ОДЗ, левая часть < 0 при x < 1, то есть неравенство выполняется при x < 1, с учетом ОДЗ получаем -4 <= х < 1. Пусть x >= 1. Возведем обе части неравенства в квадрат (x - 1)^2 < 16*(x + 4) x^2 - 2*x + 1 < 16*x + 64 x^2 - 18*x - 63 < 0 Равенство верно на интервале между корнями уравнения. Корни х1 = -3, х2 = 21, неравенство выполняется для -3 < х < 21, с учетом x >= 1 получаем 1 <= х < 21. Объединяем условия -4 <= х < 1 и 1 <= х < 21, получаем ответ: -4 <= х < 21.
Возведём в квадрат сумму или разность двучлена:
Легко запомнить. Чтобы выделить полный квадрат (квадрат двучлена) из квадратного трёхчлена, надо разделить пополам коэффициент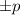
перед "х" и записать это число в скобку, которая будет возведена в квадрат ( 
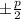), а затем вычесть квадрат этой половины, а далее приписать свободный член q. Это правило годиться, если коэффициент при 
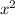равен 1. Если этот коэффициент не равен 1, то предварительно вынести его за скобку и выделять полный квадрат из выражения, записанного в скобке.
Например: