ответ: Можно.
Объяснение:
Разделим квадрат на 144 равнобедренных треугольника. ( Сначала на 36 квадратов, потом каждый квадрат двумя диагоналями на четыре равнобедренных треугольника.)
Минимально квадрат можно сложить из двух или четырех равнобедренных треугольников.
Нужны числа из которых можно извлечь корень и которые кратны 4.
Это: 4; 16; 36; 64; 100. ( для квадратов состоящих из 4 частей )
И удвоенное произведение этих чисел включая 1.
Это: 2; 8; 32; 72; 128. ( для квадратов состоящих из 2 частей )
Зная, что сумма трёх чисел равна 144, найдем количество частей в каждом из трёх квадратов. (количество частей для каждого квадрата должно быть разное)
К примеру:
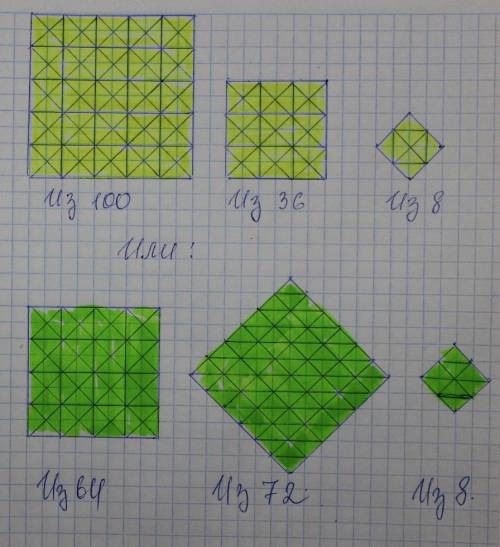
100+36+8=144
1 кв. из 100 частей ; 2 кв. из 36 частей; 3 кв. из 8 частей.
Или
64+72+8=144
1 кв. из 64 частей ; 2 кв. из 72 частей; 3 кв. из 8 частей.
Рисунок смотрите на фото.
Объяснение:
Первая труба наполняет бассейн за х часов,тогда за час - 1/х.
Вторая труба наполняет бассейн за (х+10) часов,тогда за час - 1/(х+10).
Вместе за час работы они наполнят бассейн (1/х)+ (1/(х+10)).
(1/х)+ (1/(х+10))= (х+10+х)/(х*(х+10))=(2х+10) / (х²+10х)
При совместной работе они наполняют бассейн за 12 часов:
1 ÷ (2х+10) / (х²+10х) = 12
1 * (х²+10х) / (2х+10) = 12
(х²+10х) / (2х+10) = 12
12*(2х+10) = х²+10х
24х+120-х²-10х=0
-х²+14х+120=0
х²-14х-120=0
х₁+х₂=14
х₁х₂= -120
х₁= -6 не подходит по условию
х₂=20 часов - первая труба наполняет бассейн.
20+10=30 часов - вторая труба наполняет бассейн.
b5=b1*q^4=4
b9=b1*q^8=1/4
Разделим b9 на b5 и получим q^4=1/16
q1=1/2
q2=-1/2