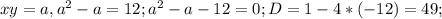
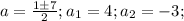, вот теперь мы можем заменить первое уравнение на более простое и решить 2 системы, объединив их решения.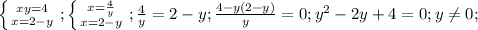 
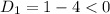, корней нет. Решаем вторую систему: 
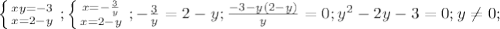Здесь b=a+c (-2=1-3), тогда 
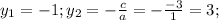, а теперь в любое уравнение подставляем каждое из получившихся и в ответе пишем 2 точки: 
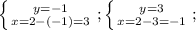, получили точки (3;-1);(-1;3). Довольно похожие значения, объясняется это всё квадратами в первом уравнении системы. ответ:(3;-1);(-1;3).
50/2=25(км/ч)-скорость сближения
пусть скорость одного велосипедиста х км/ч,тогда скорость второго (25-х) км/ч
время движения первого велосипедиста у ч,тогда время движения второго (у- 5/3) ч
составим систему уравнений :
х*(у-5/3)=50
у*(25-х)=50
ху-5/3х=50
25у-ху=50 (*)
сложим
25у-5/3х=100
5у-(1/3)х=20 умножим на 3
15у-х=60
х=15у-60
подставим в *
25у-(15у-60)у=50
25у-15у²+60у=50
-15у²+85у=50 разделим на (-5)
3у²-17у+10=0
D=289-120=169
√D=13
y1=(17-13)/6=4/6=2/3 (ч) x1=15y-60=15*(2/3)-60=10-60=-50 (км/ч) <0 -не подходит
y2=(17+13)/6=5 x2=15y-60=15*5-60=15 (км/ч)-скорость одного из велосипедистов
25-x=25-15=10 (км/ч)-скорость второго велосипедиста
ответ : 10 км/ч ; 15 км/ч.