
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
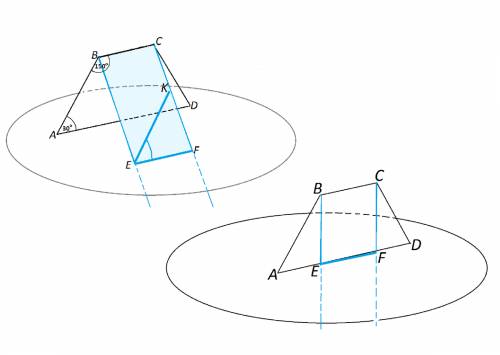
Сумма углов при боковой стороне трапеции 180°, следовательно, угол ВАD=180°-150°=30°.
Проведем в плоскости ВЕF прямую ЕК, параллельную АВ.
ЕК|║АВ; ЕF║АD Углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.⇒
∠FЕК=∠ВАD=30°
-----------
ВЕ и СF могут быть проведены в плоскости АВСD.
Тогда ЕD будет лежать на АD и в этом случае непараллельные прямые EF и АВ лежат в одной плоскости. Тогда АВ и EF пересекyтся.
ОДЗ: х принадлежит (-бесконечность; -4) U (4; +бесконечность)
для нахождения экстремума нужно найти производную...
f ' (x) = ((2x-5)(x+4) - (x^2-5x)) / (x+4)^2 = (2x^2 + 3x - 20 - x^2 + 5x) / (x+4)^2 =
= (x^2 + 8x - 20) / (x+4)^2 = (x-2)(x+10) / (x+4)^2
решение неравенства (x-2)(x+10) / (x+4)^2 > 0 (корни: -10; -4; 2)
х принадлежит (-бесконечность; -10) U (2; +бесконечность) =>
функция возрастает при х принадлежит (-бесконечность; -10] U [2; +бесконечность)
функция убывает при х принадлежит [-10; -4) U (-4; 2]
при х = -10 ---функция достигает максимума fmax = (100+50)/(-6) = -25
при х = 2 ---функция достигает минимума fmin = (4-10)/6 = -1
система:
9x - x^2 > 0
5 - x > 0
lg(5-x) не равен 0
x(9 - x) > 0
x < 5
5 - x не равно 1
х принадлежит (-бесконечность; 0) U (9; +бесконечность)
х принадлежит (-бесконечность; 5)
х не равен 4
х принадлежит (-бесконечность; 0) --- x < 0
[x]² - x*[x] + 3 ≤ 0
наименьшее положительное решение найти
x > 0
заметим что любое положительное целое значение х не решение, так как [x]² - x*[x] = 0 и 3 > 0
Немного пугает квадрат первого члена и хочется решить квадратное уравнение, но это не так. Так как [x] и [x]² это целые числа, а не переменные и у нас линейная зависимоть
[x] <= x
x = [x] + {x} целая и дробная части
0 ≤ {x} < 1
теперь будем оценивать неравенство
[x]² - x*[x] + 3 ≤ 0
[x]² + 3 ≤ x*[x]
([x]² + 3)/[x] ≤ x
имеем право [x] = 0 когда 0≤ x < 1 тогда [x]² - x*[x] = 0 и 3 > 0 не корень
[x] + 3/[x] ≤ x
x - [x] ≥ 3/[x]
{x} ≥ 3/[x]
0 ≤ {x} < 1 значит 3/[x] < 1 [x} ≥ 4 но минимум [х] = 4 то есть 4 < x < 5
{x} ≥ 3/4
{x} = 3/4 минимум
x = [x] + {x} = 4 + 3/4 = 4 3/4 = 4.75
проверяем
[4.75]² - 4.75*[4,75] + 3 = 16 - 19 + 3 = 0 ≤ 0 да
для надежности проверим два ближайших числа 4,74 и 4.76
[4.74]² - 4.74*[4,74] + 3 = 16 - 18.96 + 3 = 0.04 > 0
[4.76]² - 4.76*[4,76] + 3 = 16 - 19.04 + 3 = -0.04 < 0
ответ 4.75