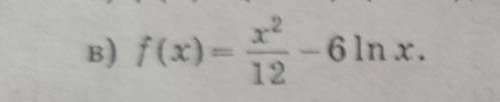
В зимние каникулы у людей появляется время на то, чтобы посещать кинотеатры. В частности, большой популярностью пользуются так называемые 5D, в которых кроме хорошего изображения и объёмного звука посетитель имеет возможность приблизиться к реальности происходящего за счёт движения кресла, ароматических эффектов и «ветра», создаваемого вентиляторами. В первые дни после Нового года, второго января, билеты купили
30
человек, затем 6 числа, после почти недели выходных, желание сходить появилось у
30
человек. Ближе к окончанию праздников, седьмого января, пощекотать себе нервы пришли уже
60
человек. Перед выходом на работу, одиннадцатого января, уже ожидалось, что не придёт никто, долговременное безделье снижает интерес к разного рода развлечениям, кроме того — это удовольствие недешёвое. Однако система скидок, которая задумана для постоянных посетителей, и ассортимент фильмов всё-таки позволили продать
600
билетов.
Для начала давайте вспомним, какие функции четные, какие нечетные, а какие ни четные, ни нечетные.
Если f(-x) = -f(x), то функция нечетная.
Если f(-x) = f(x), то функция четная.
Если же вышеперечисленные критерии не соблюдаются, то функция ни четная ни нечетная (функция общего вида).
Что же, тогда приступим.
____________________
Найдем F(-x):
F(-x) = - x³ + 4ctgx
F(-x) = - (x³ - 4ctgx)
Т.е, выполняется условие нечетной функции. f(-x) = -f(x) НЕЧЕТНАЯ
____________________
Найдем F(-x):

Не соблюдается ни одно из наших критериев. Следовательно наша функция НИ ЧЕТНАЯ НИ НЕЧЕТНАЯ.
Объяснение:
Ищем производную:
f'(x) = x/6 - 6/x = (x² - 36) / (6x) = (x - 6)(x + 6) / (6x)
f'(x) = 0
(x - 6)(x + 6) / (6x) = 0
Критические точки x = -6; x = 0; x = 6, но так как у нас x > 0 (область определения ln x), то нас интересует только x = 6
При x ∈ (0; 6], f(x) - убывает, так как f'(x) ≤ 0
x = 6 - точка минимума, так как f'(x) меняет знак с - на +
ymax = 36/12 - 6ln6 = 3 - 6ln6
При x ∈ [6; +∞) - возрастает, так как f'(x) ≥ 0