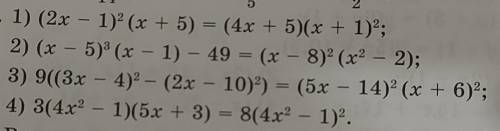
1. Записать в стандартном виде многочлен : 5х·3у²-2х²у-4ху·7у+0,5ух·5х=15ху²-2х²у-28ху²+2,5х²у=-13ху²+0,5х²у
2. Преобразовать в многочлен стандартного вида : (у³+у²-у)-(у²+у-1)=у³+у²-у-у²-у+1=у³-2у+1
3. Вычислить значение выражения : 3х²-(7ху-4х²)+(5ху-7х²) ,при х=0,3 ; у= -10
3х²-(7ху-4х²)+(5ху-7х²)=3х²-7ху+4х²+5ху-7х²=-2ху -2*0,3*(-10)=6
4.Упростить выражение : (4а²)²-2а³(1+8а)=16а^4-2а³-16a^4=-2а³
5. Упростить выражение : (а+b)(а+2)-(а-b)(а-2)-2аb=а²+2a+ab+2b-а²+2a+ab-2b-2аb=4a
6. Раскрыть скобки используя соответствующее правило : а) 3а²+(а-5)=3а²+а-5 ; б) 5-(4а+5)=5-4а-5=-4a
7. Упростить выражение : а) х-(3х+5)+(2х-4)=х-3х-5+2х-4=-9 ; б) (3а²-4b+5)+(2b-а²-1)=3а²-4b+5+2b-а²-1=2а²-2b+4
8. Решить уравнение : 3х-5+2х-7=-2
5х-12=-2
5x=10
x=2
9. Выполнить умножение: а) -4у(2х-5у+1)=-8xy+20y²-4y; б) 8а²(а-3а³)=8a³-24a^5
10. Упростить выражение : а) 5(х-8)-2(5+х)=5x-40-10-2x=3x-50 ; б) х(х²+х-2)-х²(х-1)=x³+x-2x-x³+x²=2x²-2x
11. Упростить выраж. : у²(у³+у-2)-у(у³+1)+2у²-у³ =y^5+y³-2y²-y^4-y+2y²-y³=y^5-y^4-y
^ - знак степени
ответ: 4.
Объяснение:
Одночлен со старшей степенью числителя будет иметь вид 2⁵⁰*x⁵⁰, одночлен со старшей степенью знаменателя - 2⁴⁸*x⁵⁰. Разделив числитель и знаменатель на x⁵⁰, получим в числителе выражение вида 2⁵⁰+a1/x+a2/x²+...ak/x⁵⁰, где a1, a2,..., ak - числовые коэффициенты, а в знаменателе - выражение вида 2⁴⁸+b1/x+b2/x²+...bk/x⁵⁰, где b1, b2,..., bk - также числовые коэффициенты. Так как при x⇒∞ все выражения, кроме 2⁵⁰ в числителе и 2⁴⁸ в знаменателе, стремятся к 0, то предел данной дроби равен 2⁵⁰/2⁴⁸=2²=4.
1) (4x^2-4x+1) (x+5)=(4x+5)(x^2 +2x+1)
4x^3+20x^2-4x^2-20x+x+5=4x^3 +8x^2+4x+5x^2 +10x+5
20x^2-4x^2 - 20x+x=8x^2 +4x+5x^2 +10x
16x^2-19x-13x^2-14x=0
3x^2-33x=0
3x(x-11)=0
x(x-11)=0
x-11=0
x=0
x1=0 x2=11
2) (x^3 - 15x^2+75x-125)(x-1)-49=(x^2-16x+64) (x^2-2)
x^4-x^3-15x^3+15x^2+75x^2-75x-125x+125-49=x^4-2x^2-16x^3+32x+64x^2-128
-x^3-15x^3+15x^2+75x^2-75x-125x+125-49= - 2x^2-16x^3+32x+64x^2-128
90x^2-200x+76-62x^2-32x+128=0
28x^2-232x+204=0
7x^2 - 7x-51x+51=0
7x(x-1)-51(x-1)=0
(x-1)(7x-51)=0
x-1=0
7x-51=0
x1=1 x2=51/7
3) 9(9x^2 - 24x+16)-9(4x^2 - 40x+10)=(5x^2 +30-14x-84)^2
81x^2 - 216x+144-36x^2 +360x-900=(5x^2 +16x-84)^2
45x^2 +144x-756-25x^4+584x^2 - 7056-160x^3+2688x=0
-(x-3)(x+6)(5x+31)(5x-14)=0
x1=-6,2 x2=-6 x3=2,8 x4=3
4) 3(4x^2 - 1)(5x+3)-8(4x^2 - 1)^2 =0
(4x^2 - 1)(3(5x+3)-8(4x^2 - 1))=0
(4x^2 - 1)(15x+9-32x^2 +8)=0
(4x^2 - 1)(15x+17-32x^2) =0
4x^2 - 1=0
15x+17-32x^2 =0
x1=-0,53125
x2=-0,5
x3=0,5
x4=1
Объяснение: