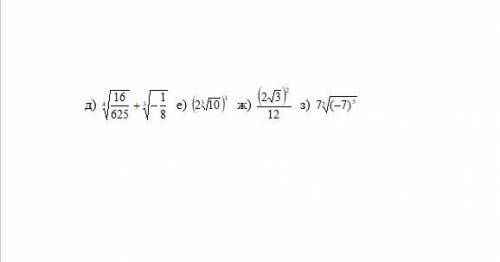
![\sqrt[4]{\dfrac{16}{625}}+\sqrt[3]{-\dfrac{1}{8}}=\sqrt[4]{\dfrac{2^4}{5^4}}+\sqrt[3]{-\dfrac{1}{2^3}}=\dfrac{2}{5}-\dfrac{1}{2}=\dfrac{4-5}{10}=-\dfrac{1}{10}=-0,1\\\\\\\Big(2\sqrt[3]{10}\Big)^3=2^3\cdot 10=8\cdot 10=80\\\\\\\dfrac{(2\sqrt{3})^2}{12}=\dfrac{2^2\cdot 3}{12}=\dfrac{12}{12}=1\\\\\\7\sqrt[5]{(-7)^5}=7\cdot (-7)=-49](/tpl/images/1537/1213/67e62.png)
Каждая сторона вписанного треугольника соединяет середины сторон исходного и поэтому является средней линией. Средняя линия треугольника равна половине длины стороны, которой она параллельна.
Коэффициент k подобия этих треугольников ½
.Отсюда каждая сторона первого вписанного треугольника равна 8·½ =4 см
.Пусть периметр исходного треугольника будет Р₁,
периметр первого вписанного треугольника- р₂
Тогда Р₁=8·24 см
р₂=24·½ =12 cм
Отношение периметров подобных треугольников равно коэффициенту их подобия.
р₃=12·½=6 см
р₄=6·½=3 см
р₅=3·½=1,5 см
р₆=1,5·½=0,75 см
р₇=0,75·½=0,375 см
р₈=0,375·½=0,1875 см
Как Вы, наверное, обратили внимание, последовательность периметров сторон вписанных треугольников - геометрическая прогрессия, где каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число ½.
Каждый член геометрической прогрессии {bn} определяется формулой
bn = b₁ · qⁿ⁻¹
b₈=24·(½)⁷=0,1875 см