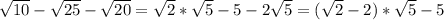
y = - x³ + 3x² + 4
Найдём производную :
y' = (- x³)' + 3(x²)' + 4' = - 3x² + 6x
Приравняем производную к нулю , найдём критические точки :
- 3x² + 6x = 0
- 3x(x - 2) = 0
x₁ = 0
x - 2 = 0 ⇒ x₂ = 2
Обе критические точки принадлежат заданному отрезку. Найдём значения функции в критических точках и на концах отрезка и сравним их .
y(- 3) = -(- 3)³ + 3 * (- 3)² + 4 = 27 + 27 + 4 = 58
y( 3) = - 3³ + 3 * 3² + 4 = - 27 + 27 + 4 = 4
y( 0) = - 0³ + 3 * 0² + 4 = 4
y(2) = - 2³ + 3 * 2² + 4 = - 8 + 12 + 4 = 8
Наименьшее значение функции равно 4, а наибольшее равно 58 .
Если основание больше нуля, но меньше 1, то функция у=аˣ убывает, чем меньше показатель, тем функция больше, и наоборот, чем показатель больше. тем функция меньше, при основании больше единицы функция возрастает, чем больше показатель, тем функция больше, и наоборот. чем меньше. тем меньше функция.
1) 4) и 6) возрастающие функции, поэтому если положить 1=(4/3)⁰, то
1)
(4/3)²/³>1=(4/3)⁰, т.к. 2/3>0
4)
(7/6)⁻¹/²<1=(7/6)⁰
6)
3.14 ⁻⁰.⁴ <1=3.14⁰
Остальные функции убывают, поэтому 2)
(3/4)²/³< 1=(3/4)⁰
3)
(6/7) ⁻¹/² >1=(3/7)⁰
5)
0.62⁻⁰.⁴>1=0.62⁰