X1=2
X2=-5/9
Объяснение:
(-3x)²-13x-10=0
9x²-13x-10=0
D=169-4*9*(-10)=529=23²
X1=(13+23)/18=2
X2=(13-23)/18=-10/18=-5/9
X(t) = t² - 3t, tо = 4
Среднюю скорость движения на указанном отрезке времени;
Средняя скорость движения определим по формуле
Vcp= /frac{/Delta x}{/Delta t}
Δx=X(4)-X(0)=4²-3*4-0=16-12=4
Δt=4
Vcp= /frac{4}{4} =1
Скорость и ускорение в момент времени tо=4
Скорость точки в момент времени t определяется через производную перемещения
V(t) = X(t) =(t²-3t)=(t²)-(3t)=2t-3
V(4)=2*4-3=5
Ускорение точки в момент времени t определяется через производную скорости
а(t) =V(t)=(2t-3)=2
Моменты остановки
В момент остановки скорость равна нулю
V(t) = 0
2t - 3 = 0
2t = 3
t = 1,5
продолжает ли точка после момента остановки двигаться в том же направлении или начинает двигаться в противоположном направлении;
В противоположном направлении так как знак скорости изменился на противоположный.
Наибольшую скорость движения на указанном отрезке времени.
Скорость движения на концах отрезка времени
V(0) = 2*0 - 3 = -3
V(4) = 2*4 - 3 = 8 - 3 = 5
Найдем производную(ускорение) функции скорости от времени
V(t) = (2t - 3) = 2
Постоянная величина производной (ускорения) говорит о том что движение равноускоренное и максимум и минимум скорости находится на концах отрезка.
Поэтому максимальноя скорость на отрезке находится в момент времени t = 4 и равна Vmax = V(4) = 5
Запишем эту сумму для произвольного числа слагаемых:
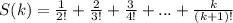
Вычислим значения S(k) для нескольких значений k:
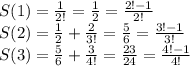
Тогда можно предположить, что
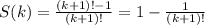
Но это ещё надо доказать. Используем индукцию. Выше было показано, что равенство верно для первых 3 натуральных k. Докажем, что из справедливости равенства для k=n следует справедливость равенства для k=n+1, тогда равенство можно будет считать справедливым для всех натуральных k.
Итак, предположим, что справедливо равенство
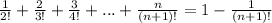
Проверим, верно ли, что
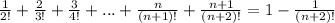
Подставляем сюда предыдущее выражение:
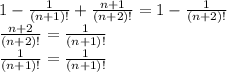
Получили верное равенство. Теперь можно вычислить значение нашей суммы:
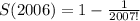
вот так вроде бы правильно