Question

Объясните подробно, как делать подобные : найдите значение выражения: квадратный корень 8-2√7(здесь корень заканчивается)-√7

Answer 1

$\sqrt{ 8-2\sqrt{ 7}} - \sqrt{ 7}$

тут мы иммем дело с разницей квадрата под корнем. его надо уметь видеть.

$(a+b)^{2}$ = $a^{2}$ + 2ab + $b^{2}$

$(a-b)^{2}$ = $a^{2}$ - 2ab + $b^{2}$

в данном случе второе(минус перед два корней из семи).

И так 2√7 - в данном случае это у нас 2ab.

8 - это сума а в квадрате и б в квадрате.

то есть:

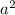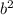
8 =  $a^{2}$ + $b^{2}$

2ab = 2√7

ab = √7

То есть нам нужно методом подбора подобрать такие числа, чтобы их сумма в квадрате была 8, а при умножении они давали корень из семи. (тут метод подбора ничего более просто нужны тренировки и практика для этого).

Я подобрала:

$\sqrt{7}$ и 1. И в правду, $\sqrt{7}$ * 1 =[/tex]\sqrt{7}[/tex]

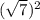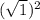и $(\sqrt{7})^{2}$ + $(\sqrt{1})^{2}$ = 7 + 1 = 8

то есть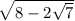 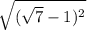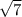$\sqrt{8-2\sqrt{ 7}}$ = $\sqrt{(\sqrt{ 7} - 1)^{2}}$ = |$\sqrt{ 7}$ - 1| (по модулю, модуль убираем, ибо $\sqrt{ 7} 1;$|$\sqrt{ 7} - 1| = \sqrt{7} - 1$

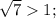То есть:

$\sqrt{8-2\sqrt{ 7}}- \sqrt{7}$ =  $\sqrt{ 7}$ - 1  - $\sqrt{ 7}$ = -1.

ответ: -1.

Answer 2

$\sqrt{8-2\sqrt7}-\sqrt7=\sqrt{(\sqrt1)^2-2\sqrt7+(\sqrt7)^2}-\sqrt7= \\ \\ = \sqrt{(\sqrt1-\sqrt7)^2}-\sqrt7=[1-\sqrt7]-\sqrt7=\sqrt7-1-\sqrt7=-1$