Объяснение:
=(x+2)^2-4 - квадратичная функция, график - парабола, ветви направлены вверх, график можно получить путём параллельного переноса графика функции y=x^2 на 2 единичных отрезка влево и на 4 единичных отрезка вниз
1) D(y)=R
2) Нули: x=0 при y=0; y=0 при x=0 и x=-4
3) y<=0 при x принадлежащем [-4;0], y>0 при x принадлежащем (-бесконечность;-4) и (0;+ бесконечность)
4) Функция убывает на промежутке x принадлежащем (-бесконечность;-2) и возрастает на промежутке x принадлежащем (-2;+ бесконечность)
5) E(y)=[-4;+бесконечность).
В решении.
Объяснение:
Решить графически:
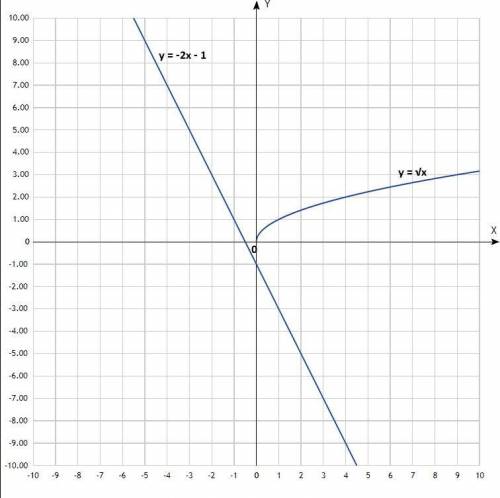
√х = -2х - 1
↓
у = √х; у = -2х - 1;
Построить графики.
Первый - ветвь параболы; второй - прямая линия.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = √х; у = -2х - 1;
Таблицы:
х 0 1 4 9 х -1 0 1
у 0 1 2 3 у 1 -1 -3
По вычисленным точкам построить графики.
Графики не имеют точек пересечения, значит,
уравнение не имеет действительных корней.
24a³b⁴c-12a²b⁴c²+6a²b³=6a²b³(4abc-2bc²+1)