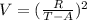Все просто, имеем:
T=A+R/√V;
Чтобы выразить V нужно для начала привести к общему знаменателю всю формулу (Знаменатель опускается):
T*√V=A*√V+R;
Далее, переносим все что связано с √V в левую сторону, R оставляем в правой стороне.
T*√V-A√V=R;
Далее, группируем, вынося √V за скобку.
√V*(T-A)=R;
Далее, делим правую часть на левую. Тем самым, мы вывели величину V:
√V=R/(T-A)
Избавляемся от корня, возводя обе части в квадрат:
V=R^2/(T-A)^2;
Вот и вся задача.
49x²-84x+a=0
D= (-84)² - 4*49a
D=7056 - 196a
Есть 3 возможных случая: D>0, D=0, D<0
{ 7056 - 196a > 0
{ 7056 - 196a = 0
{ 7056 - 196a < 0
Принимай эти три скобки, как одну большую.
Решить все три уравнения:
7056 - 196а > 0
-196а > -7056
−7 056/(−196)
а=36
Точно так решить все:
{а<36
{а=36
{а>36
Осталось определить количество корней:
{а<36 , 2 действительных корня
{а=36 , 1 действительный корень
{а>36 , нет действительных корней
При значении а=36, уравнение имеет единственный действительный корень

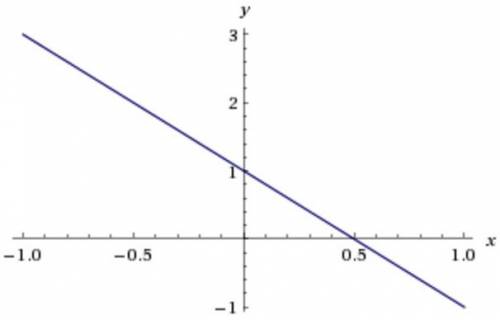
Если формула такая
то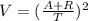
Если формула такая
то