Для нахождения решения корней x2 - 6x = 16 полного квадратного уравнения мы начнем с того, что перенесем 16 в левую часть уравнения:
x2 - 6x - 16 = 0.
Для решения уравнения будем использовать формулы для поиска дискриминанта и корней уравнения через дискриминант.
D = b2 - 4ac = (-6)2 - 4 * 1 * (-16) = 36 + 64 = 100;
Корни уравнения мы вычислим по следующим формулам:
x1 = (-b + √D)/2a = (6 + √100)/2 * 1 = (6 + 10)/2 = 16/2 = 8;
x2 = (-b - √D)/2a = (6 - √100)/2 * 1 = (6 - 10)/2 = -4/2 = -2.
ответ: x = 8; x = -2.
Объяснение:
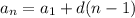
sin105+sin75=sin(90+15)+sin(90-15)=cos15+cos15=2cos15
cos15=±sqrt [(1+cos30)/2 ] =±sqrt [ (1+√3/2)/2 ]=±sqrt [(2+√3) ]/2
Выбираем знак +, так как 15 градусов - это угол 1 четверти, косинусы этих углов положительны.
√(2+√3)
2cos15=2* = √(2+√3)
2
2) Рассмотрим выражение ( √tga +√ctga)²=tga+2√tga*√ctga +ctga=
=(tga+ctga)+2√(tga*ctga)= a+2*√1= a+2