×^2(1+3×)
Объяснение:
это правилно
1) x ∈ (-∞; -8) U (3; +∞)
2) x ∈ (-∞; -3) U (5; 7)
Объяснение:
1) x^2 + 5x - 24>0
x^2 + 5x - 24=0
D= √(b^2 - 4ac) = √(5^2 - 4 * 1 * (-24)) = √(25 + 96) = √121 = 11
x = (-b +/- √D)/2a
x1 = -5 + 11 / 2 =3
x2 = -5-11 /2 = -8
Получается три интервала:
x<-8
-8<x<3
x>3
чередуем знаки справа налево, первый - плюс (так как нам нужно больше, то выбираем там, где плюс)
получаем x<-8 и x>3
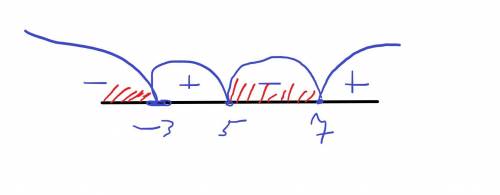
2) (x-5)(x-7)(x+3)<0
(x-5)(x-7)(x+3)=0
x = 0 тогда, когда один из множителей равен нулю:
x=5; x=7; x=-3
получаем четыре интервала (см фотку)
выбераем там, где минус, т. к. нужен знак < по условию
x<-3 и 5<x<7
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
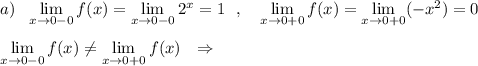
При х=0 функция имеет разрыв 1 рода .
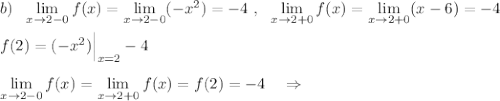
При х=2 функция непрерывна.
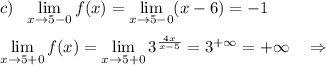
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
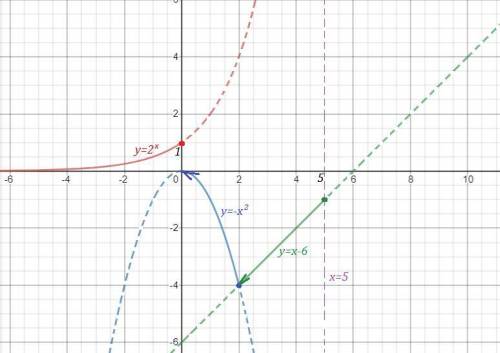
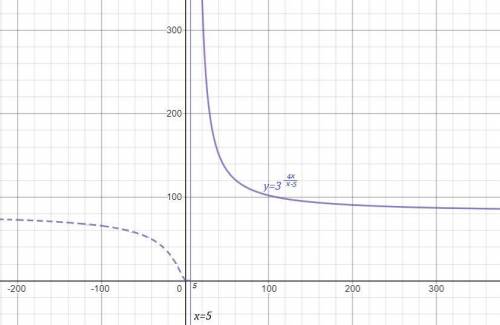
На 1 рисунке нет чертежа функции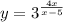 
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
x^2(1+3x)
Объяснение:
т.к их общий множитель - это x^2