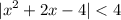
раскроем модуль:
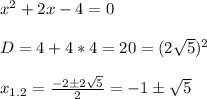
_+___ -1 -√5 ___-___ -1+√5__+__
x²+2x-4 -x²-2x+4 x²+2x-4
1) теперь рассмотрим решение неравенства на промежутках
(-∞; -1-√5] ∪ [-1+√5; +∞)
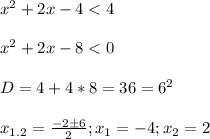
_\\\\\\ -4 _\\\\\ -1-√5_____ -1+√5_\\\\\\_ 2__\\\\\__
////////////////////////////////////////////////
пересечением решений будут промежутки
(-4; -1-√5] ∪ [-1+√5;2)
2) теперь рассмотрим решение неравенства на промежутках
(-1-√5;-1+√5)
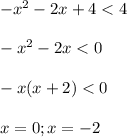
_____ -1-√5_ \\\\\\_ -2_\\\\\\_ 0_\\\\\_-1+√5_____
//////////////////////////// /////////////////////
пересечением решений будут промежутки (-1-√5;-2) ∪ (0; -1+√5)
И Тогда общим ответом будет
(-4; -2) ∪ (0;2)
a1=13;b1=13;a2=17;b2=17
Объяснение:
берем формулы площади и периметра прямоугольника и используем их для создания системы уравнений
S=ab=221
P=2(a+b)=60
система ab=221
2(a+b)=60
с нижнего уравнения выражаем ,к примеру b:
2a+2b=60
a+b=30
b=30-a
и подставляем выраженную b в первое уравнение из системы,в итоге получаем квадратное уравнение :
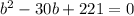
вычисляем дискриминант :
D=-b+4ac=900-884=16 (±4)
вычисляем b1 и b2:
b1=(30+4)/2=17
b2=(30-4)/2=13
теперь найденные b подставляем вот сюда: b=30-a и находим а:
a1=13 a a2=17
А) 2x^2-18=0 2x^2=18 x^2=18/2=9 x=3 ; -3 Б) 5x^2+15x=0 x(5x+15)=0 x1=0 5x+15=0 5x=-15 X2=-3 В) x^2+5=0 x^2=-5 Корней нет Г) 6x^2-12=0 6x^2=12 x^2=2 x=√2; -√2 Д) 3x^2+12x=0 x(3x+12)=0 x1=0 3x+12=0 3x=-12 x=-4 Е) 7+x^2=0 x^2=-7 Корнет нет
Объяснение: