7x²=21x
Перенести условия в левую часть
72=21
72−21=0
Простой фактор
72=21
7(2−3)=0
Разделите обе части уравнения на один и тот же член
7(2−3)=0
2−3=0
Используйте формулу корней квадратного уравнения
=−±2−4/√2
Приведите уравнение к общему виду, определите коэффициенты a, b и c, затем вставьте их в формулу.
2−3=0
=1
b=-3
=0
=−(−3)±√(−3)2−4⋅1⋅0/2⋅1
Упростите
Возведите в степень
Умножьте на ноль
Сложите числа
Вычислите квадратный корень
Умножьте числа
x=3±3/2
Разделите уравнение
Чтобы найти неизвестное, разложите уравнение на два: одно – с плюсом, другое – с минусом.
=3+3/2
=3−3/2
Найдите значения
Чтобы решить уравнение, преобразуйте его и вычислите неизвестное.
=3
=0
9x²=27x
Перенести условия в левую часть
92=27
9x^{2}=27x9x2=27x
92−27=0
Простой фактор
92−27=0
9x^{2}-27x=09x2−27x=0
9(2−3)=0
9(x^{2}-3x)=09(x2−3x)=0
Разделите обе части уравнения на один и тот же член
9(2−3)=0
9(x^{2}-3x)=09(x2−3x)=0
2−3=0
Используйте формулу корней квадратного уравнения
=−±2−4/√2
Приведите уравнение к общему виду, определите коэффициенты a, b и c, затем вставьте их в формулу.
²−3=0
=1
=−3
=0
=−(−3)±√(−3)²−4⋅1⋅0/2⋅1
Упростите
Возведите в степень
Умножьте на ноль
Сложите числа
Вычислите квадратный корень
Умножьте числа
=3±3/2
Разделите уравнение
Чтобы найти неизвестное, разложите уравнение на два: одно – с плюсом, другое – с минусом.
=3+3/2
=3−3/2
Найдите значения
Чтобы решить уравнение, преобразуйте его и вычислите неизвестное.
=3
=0
х - у = 8
х + у = - 3
Выразим у из каждого уравнения:
у = х - 8
у = - х - 3
Построим графики двух этих функций. Это линейные функции, графиком являются прямые. Для построения каждой прямой надо знать две точки.
у = х – 8
х1 = 0 х2 = 1
у1 = -8 у2 = -7
(0; -8) (1; -7)
у = - х - 3
х1 = 0 х2 = 1
у1 = - 3 у2 = -4
(0; -3) (1; -4)
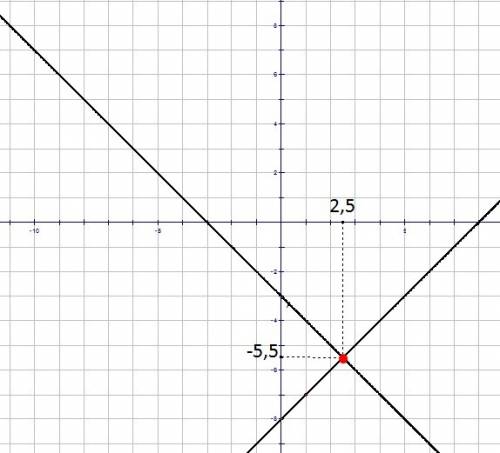
По данным точкам строим две прямые. Находим точку пересечения. Координаты точки пересечения будут ответом в данной системе.
х = 2,5
у = -5,5
Чертёж прилагается.
ответ: (2,5; -5,5)