Согласно определению периодической функции, функция f (x) является периодической, а число Т ≠ 0 ее периодом, если для любых значений переменной х выполняется равенство f(x) = f(x + Т).
1) f(x) = sin x/4,T = 8π.
Используя тот факт, что функция sin x является периодической с периодом 2π, получаем:
sin ((x + 8π)/4) = sin (x/4 + 8π/4) = sin (x/4 + 2π) = sin (x/4).
Следовательно, функция f(x)=sin x/4 является периодической с периодом 8π.
2) f (x) = 3cos2x, T = π.
Используя тот факт, что функция cos x является периодической с периодом 2π, получаем:
3cos(2 * (x + π)) = 3cos(2 * x + 2 * π) = 3cos(2 * x) = 3cos2х.
Следовательно, функция f (x) = 3cos2x является периодической с периодом π.
3) f(x) = tg3x, T= π/3.
Используя тот факт, что функция tg x является периодической с периодом π, получаем:
tg(3 * (x + π/3)) = tg(3 * x + 3π/3) = tg(3x + π) = tg3x.
Следовательно, функция f (x) = tg3x является периодической с периодом π/3.
4) f(x) = ctg x/4, T = 4π.
Используя тот факт, что функция сtg x является периодической с периодом π, получаем:
сtg((х + 4π)/4) = ctg(x/4+ 4π/4) = ctg(x/4 + π) = ctgx/4.
Следовательно, функция f (x) = ctg x/4 является периодической с периодом 4π.
:3
Распишем модуль:
Уравнения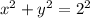
и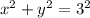 
- уравнения окружности.
Неравенство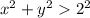
определяет часть плоскости вне окружности с радиусом 2.
Неравенство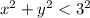
определяет часть плоскости внутри окружности с радиусом 3.
Значит, неравенство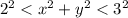
определяет кольцо, ограниченное окружностями с радиусами 2 и 3.