Відповідь:
Шість головних діагоналей дорівнюють подвоєній стороні шестикутника.
Шість додаткових діагоналей дорівнюють стороні шестикутника помноженій на корень квадратний із трьох.
Пояснення:
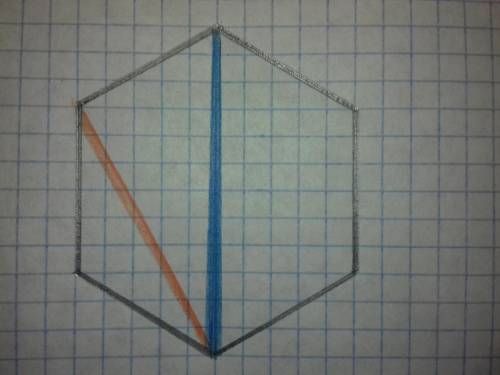
У правильному шестикутнику є шість головних діагоналей, що проходять крізь його геометричний центр ( центр описаної та вписаної окружності ), одна з них намальована синім кольором на малюнку. Довжина цієї діагоналі дорівнює подвоєній стороні шестикутника. Тому, що у правильному шестикутнику сторона дорівнює радіусу описаної окружності, а діагональ дорівнює двом радіусам.
Існує ще шість додадкових діагоналей, що не проходять крізь центр шестикутника, одна з таких діагоналей намальована червоним кольором на малюнку. Довжина такої діагоналі дорівнює стороні шестикутника помноженій на корень квадратний із трьох. Тому, що ця діагональ утворює рівнобічний трикутник з кутом при основі 30°, а основа трикутника дорівнює стороні шестикутника помноженій на 2 × cos (30°) = sqrt (3).
Объяснение:
a1=3
a3=9
а2 = (3+9) /2 = 6
d = а2-а1 = 6 - 3 = 3
a10 = a1 + (10-1) *d = 3 + (10-1) *3 = 3 + 9*3 = 30
S = (a1+a10)/2 * 10 = (3+30)/2 *10 = 165