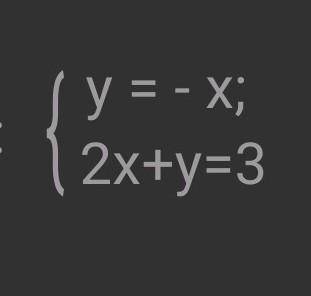
|5x-3|+|3x-5|=9x-10
Из определения модуля следует, что |a|>=0, |a|+|b|>=0
Отсюда:
9x-10>=0 <=> x>=10/9$ при x<10/9 корней нет
Найдем иные границы интервалов раскрытия модулей:
5x-3=0 <=> х=3/5 < 10/9
3x-5=0 <=> x=5/3>10/9/
3/5 10/9 5/3
|||>x
КОРНЕЙ НЕТ!
Отсюда: при x<10/9 - корней нет
При
10/9<= х <=5/3 имеем:
5x-3+(-3x+5)=9x-10
2x+2=9x-10
x=12/7
сравним 12/7 и 5/3:
12/7=36/21 > 5/3=35/21 => корень не входит интервал
При 10/9<= х <=5/3 корней нет
При x>=5/3
5x-3+3x-5=9x-10
8x-8=9x-10
- x = - 2
x=2
x=2 > 5/3, этот корень в исследуемый интервал входит.
ответ х=2
1)Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной величине отрицательного показателя: а – n = ( 1 / an )
2)Степень любого ненулевого числа с нулевым показателем равна 1:
a^0 = 1
Например: 2^0 = 1, (-5)^0 = 1, (3 / 5)^0 = 1
3)При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
am · an = am + n ,
где «a» — любое число, а «m», «n» — любые натуральные числа.
Пример:
b · b2 · b3 · b4 · b5 = b 1 + 2 + 3 + 4 + 5 = b15