1. 4y^2+14y+12
2. 8a^2-2ab-15b^2
3. a^3-b^3
4. 8a^3+2a^2-15a
Объяснение:
1. (2y+4)(2y+3)=4y^2+6y+8y+12=4y^2+14y+12
2. (2a-3b)(4a+5b)=8a^2+10ab-12ab-15b^2=8a^2-2ab-15b^2
3. (a-b)(a²+ab+b²)=a^3-b^3 (формула сокращённого умножения)
4. a(4a-5)(2a+3)=a(8a^2+12a-10a-15)=a(8a^2+2a-15)=8a^3+2a^2-15a
Напомним основные свойства степени. Пусть а > 0, b > 0, n, m - любые действительные числа. Тогда
1) an am = an+m
2)
a
n
a
m
=
a
n
−
m
3) (an)m = anm
4) (ab)n = an bn
5)
(
a
b
)
n
=
a
n
b
n
6) an > 0
7) an > 1, если a > 1, n > 0
8) an < am, если a > 1, n < m
9) an > am, если 0< a < 1, n < m
В практике часто используются функции вида y = ax, где a - заданное положительное число, x - переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = ax, где а — заданное число, a > 0,
a
≠
1
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень ax где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение ax = b, где а > 0,
a
≠
1
, не имеет корней, если
b
≤
0
, и имеет корень при любом b > 0.
3) Показательная функция у = ax является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 < a < 1.
Это следует из свойств степени (8) и (9)
Построим графики показательных функций у = ax при a > 0 и при 0 < a < 1.
Использовав рассмотренные свойства отметим, что график функции у = ax при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х < 0 и |х| увеличивается, то график быстро приближается к оси Oх (но не пересекает её). Таким образом, ось Ох является горизонтальной асимптотой графика функции у = ax при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = ax при 0 < a < 1 также проходит через точку (0; 1) и расположен выше оси Ох.
Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х < 0 и |х| увеличивается, то график быстро поднимается вверх.
Смотри в файле
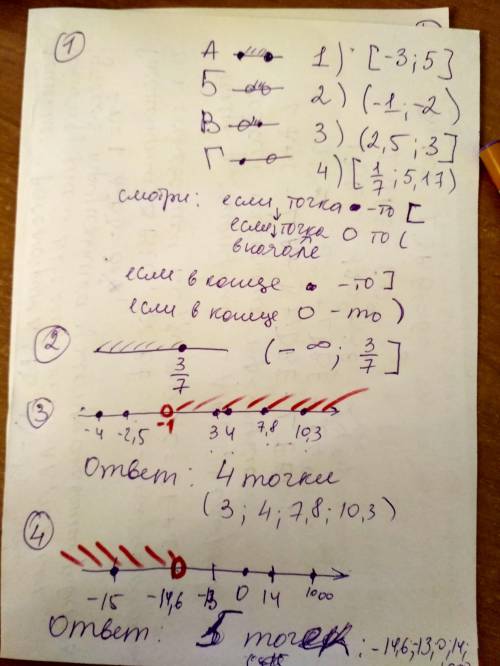
Смотри : есть всего 4 варианта точек и скобочек:
если точка закрашена и в начале отрезка( слева) , то скобочка [
если точка закрашена и в конце отрезка( справа) , то скобочка ]
если точка пустая в середине и в начале отрезка , то скобочка (
если точка пустая в середине и в конце отрезка( справа) , то скобочка )
остальное в файлах
если закрашена( значит точка принадлежит отрезку и будут такие знаки математические ≥ ≤ больши и равно , меньше и равно)
если пустая точка( то не принадлежит этому отрезку и знаки математические > < ,"Больше" или "меньше")
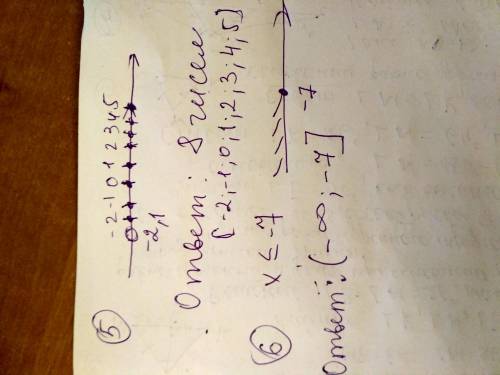
Объяснение:
1) 4у²+14у+12
2) 8а²-2аb-15b²
3) a³-b³
4) 8a³+2a²-15