1)18 (машин на второй стоянке)
36 (машин на первой стоянке)
29 (машин на третьей стоянке)
2)10 (бочек на втором стеллаже)
27 (бочек на третьем стеллаже)
81 (бочка на первом стеллаже)
Объяснение:
1. На трёх стоянках 83 автомобиля, на первой в два раза больше, чем на второй, а на третьей на 7 машин меньше , чем на первой. Сколько машин на каждой стоянке?
1)х - машин на второй стоянке
2х - машин на первой стоянке
2х-7 - машин на третьей стоянке.
По условию задачи всего 83 машины, уравнение:
х+2х+2х-7=83
5х=83+7
5х=90
х=90/5
х=18 (машин на второй стоянке)
18*2=36 (машин на первой стоянке)
36-7=29 (машин на третьей стоянке)
Проверка:
18+36+29=83 (маш.)
2) На трёх стеллажах 118 бочек, причём на третьем в три раза меньше , чем на первом и на 17 больше чем втором. Сколько бочек на каждом стеллаже?
х - бочек на втором стеллаже
х+17 - бочек на третьем стеллаже
3(х+17) - бочек на первом стеллаже
По условию задачи всего 118 бочек, уравнение:
х+х+17+3(х+17)=118
2х+17+3х+51=118
5х=118-68
5х=50
х=10 (бочек на втором стеллаже)
10+17=27 (бочек на третьем стеллаже)
27*3=81 (бочек на первом стеллаже)
Проверка:
10+27+81=118.
у(наиб) = 32 ( в точке х=2)
у(наим) = 5 ( в точке х=1)
На границах интервала.
Объяснение:
Для того, чтобы найти наибольшее и наименьшее значение функции нам необходимо:
Найти все стационарные точки.Найти все критические точки. Проверить границы интервала. Пункт 1 - стационарные точки:Данные точки ищутся с производной. Найдем производную данной функции:
x'(t) = 8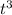
- 3.
Приравниваем производную к 0:
8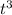
- 3 = 0
t = ±![\sqrt[3]{\frac{3}{8} }](/tpl/images/1201/0058/69c06.png)
= ±![\frac{\sqrt[3]{3} }{2}](/tpl/images/1201/0058/4c079.png)
- однако, эти точки не входят в наш интервал.
Пункт 2 - критические точки:Таковых у нас нет, т.к. критические точки - это стационарные точки, но которые не входят в ОДЗ. (У нас ОДЗ от (-∞;∞+)).
Пункт 3 - границы графика:Подставляем значения границ интервала и находим значения в этих точках:
x(1)=2*1^4−3*1+6 = 5
x(2)=2*2^4−3*2+6 = 32
Следовательно, это и есть наибольшее и наименьшее значение функции на заданном интервале.