Как данный эпизод понять характер героини? Теперь посмотрим, что делает, оставшись одна, красавица дочка. Оксане не минуло еще и семнадцати лет, как во всем почти свете, и по ту сторону Диканьки, и по эту сторону Диканьки, только и речей было, что про нее. Парубки гуртом провозгласили, что лучшей девки и не было еще никогда и не будет никогда на селе. Оксана знала и слышала все, что про нее говорили, и была капризна, как красавица. Если бы она ходила не в плахте и запаске, а в каком-нибудь капоте, то разогнала бы всех своих девок. Парубки гонялись за нею толпами, но, потерявши терпение, оставляли мало-помалу и обращались к другим, не так избалованным. Один только кузнец был упрям и не оставлял своего волокитства, несмотря на то что и с ним поступаемо было ничуть не лучше, как с другими.
По выходе отца своего она долго еще принаряживалась и жеманилась перед небольшим в оловянных рамках зеркалом и не могла налюбоваться собою. «Что людям вздумалось расславлять, будто я хороша? — говорила она, как бы рассеянно, для того только, чтобы об чем-нибудь поболтать с собою. — Лгут люди, я совсем не хороша». Но мелькнувшее в зеркале свежее, живое в детской юности лицо с блестящими черными очами и невыразимо приятной усмешкой, прожигавшей душу, вдруг доказало противное. «Разве черные брови и очи мои, — продолжала красавица, не выпуская зеркала, — так хороши, что уже равных им нет и на свете? Что тут хорошего в этом вздернутом кверху носе? и в щеках? и в губах? Будто хороши мои черные косы? Ух! их можно испугаться вечером: они, как длинные змеи, перевились и обвились вокруг моей головы. Я вижу теперь, что я совсем не хороша! — и, отодвигая несколько подалее от себя зеркало, вскрикнула: — Нет, хороша я! Ах, как хороша! Чудо! Какую радость принесу я тому, кого буду женою! Как будет любоваться мною мой муж! Он не вспомнит себя. Он зацелует меня насмерть».
— Чудная девка вошедший тихо кузнец, — и хвастовства у нее мало! С час стоит, глядясь в зеркало, и не наглядится, и еще хвалит себя вслух!
«Да, парубки, вам ли чета я? вы поглядите на меня, — продолжала хорошенькая кокетка, — как я плавно выступаю; у меня сорочка шита красным шелком. А какие ленты на голове! Вам век не увидать богаче галуна! Все это накупил мне отец мой для того, чтобы на мне женился самый лучший молодец на свете!» И, усмехнувшись, поворотилась она в другую сторону и увидела кузнеца…
Вскрикнула и сурово остановилась перед ним.
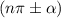 , где
, где 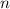 — целое число, то вид тригонометрической функции не меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например,
— целое число, то вид тригонометрической функции не меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например, 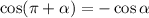 (минус, потому что общий угол будет находиться в третьей четверти).если в тригонометрической формуле встречается выражение
(минус, потому что общий угол будет находиться в третьей четверти).если в тригонометрической формуле встречается выражение 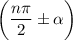 , где
, где 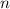 — целое число, то вид тригонометрической функции меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например,
— целое число, то вид тригонометрической функции меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например, 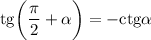 (минус, потому что общий угол будет находиться во второй четверти).
(минус, потому что общий угол будет находиться во второй четверти).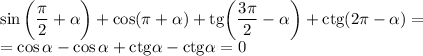
Чтобы получить решение квадратного уравнения графическим Квадратное уравнение разделяют на две функции, линейную и квадратичную. А затем строят графики этих функций на одной координатной плоскости.
Квадратное уравнение
1.ax2+bx+c=0разбивают на две функции
2.y1=ax23.y2=−(bx+c)Функция y1 это парабола. Функция y2 это прямая линия. Решением, корнями квадратного уравнения являются точки пересечения этих функций.
При решении могут представиться три варианта:
Функции имеют две точки пересечения - два корня квадратного уравнения действительны и различны между собой.Функции имеют одну точку пересечения - квадратное уравнение имеет только один действительный корень.Функции не имеют ни одной точки пересечения - тогда оба корня квадратного уравнения мнимые, комплексные числа.