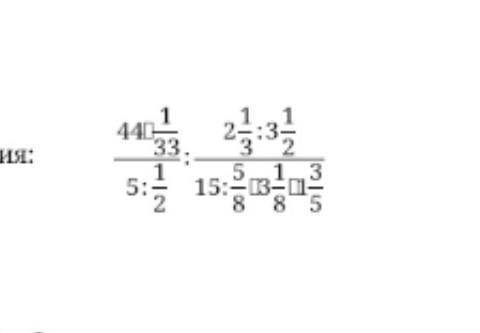
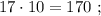
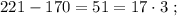
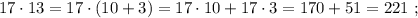
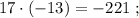
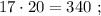
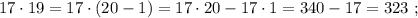
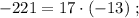
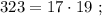
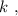каждое из которых представляет собой какое-то допустимое нечётное число, умноженное на 17, тогда можно сложить все эти допустимые нечётные числа и умножить их на 17 (вынести за скобку общий множитель).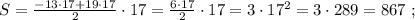
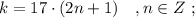
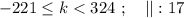
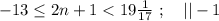
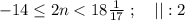
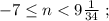
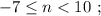
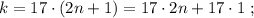
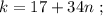
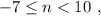который пробегает 
разных значений.![S = \frac{ [ 17 + 34 \cdot (-7) ] + [ 17 + 34 \cdot 9 ] }{2} \cdot 17 = \frac{ 2 \cdot 17 + 34 \cdot ( -7 + 9 ) }{2} \cdot 17 = \\\\ = ( 17 + \frac{ 34 \cdot 2 }{2} ) \cdot 17 = ( 17 + 17 \cdot 2 ) \cdot 17 = 17^2 \cdot 3 = 289 \cdot 3 = 867 \ ;](/tpl/images/0532/7209/6e09f.png)
1) Формула, задающая линейную функцию, имеет вид у = kx + b.
Так как прямая параллельна прямой у = - 2x +7, то угловые коэффициенты прямых равны, k = - 2, формула имеет вид у = - 2х + b.
2) Прямая у = - 2х + b проходит через точку А( - 2; - 4), тогда
- 4 = - 2•(-2) + b
- 4 = 4 + b
- 4 - 4 = b
- 8 = b
Формула примет вид: у = - 2х - 8.
ответ: у = - 8 - 2х.
2) у = (х - 3)² - (х - 2)(х + 4)
у = х² - 6х + 9 - (х² + 4х - 2х - 8) = х² - 6х + 9 - х² - 4х + 2х + 8 = - 8х + 17.
у = - 8х + 17
k = - 8; b = 17.
ответ: k = - 8; b = 17.
СКАЧАЦ приложение дроби