Объяснение:
1)
{ x^2 + xy = 2
{ y - 3x = 7
Решаем заменой
{ y = 3x + 7
{ x^2 + x(3x + 7) = 2
Решаем 2 уравнение
x^2 + 3x^2 + 7x - 2 = 0
4x^2 + 7x - 2 = 0
D = 7^2 - 4*4*(-2) = 49 + 32 = 81 = 9^2
x1 = (-7 - 9)/8 = -16/8 = -2; y1 = 3x + 7 = -6 + 7 = 1
x2 = (-7 + 9)/8 = 2/8 = 1/4; y2 = 3x + 7 = 3/4 + 7 = 7 3/4 = 31/4
ответ: (-2; 1); (1/4; 7 3/4)
2)
{ x^2 + y^2 = 16
{ x + y = 4
Возводим в квадрат 2 уравнение
{ x^2 + y^2 = 16
{ (x + y)^2 = 4^2
Раскрываем скобки
{ x^2 + y^2 = 16
{ x^2 + 2xy + y^2 = 16
Подставляем 1 уравнение во 2 уравнение
16 + 2xy = 16
2xy = 0
x = 0, y1 = 4, y2 = -4 - не подходит под 2 уравнение
y = 0, x1 = 4, x2 = -4 - не подходит под 2 уравнение
ответ: (4; 0); (0; 4)
3)
{ (x - 1)(y - 1) = 2
{ x + y = 5
Решаем заменой
{ y = 5 - x
{ (x - 1)(5 - x - 1) = 2
Решаем 2 уравнение
(x - 1)(4 - x) - 2 = 0
-x^2 + 5x - 4 - 2 = 0
Умножаем на -1
x^2 - 5x + 6 = 0
(x - 2)(x - 3) = 0
x1 = 2; y1 = 5 - x = 5 - 2 = 3
x2 = 3; y2 = 5 - x = 2
ответ: (2; 3); (3; 2)
4)
{ (x - 2)(y + 1) = 1
{ x - y = 3
Решаем заменой
{ y = x - 3
{ (x - 2)(x - 3 + 1) = 1
Решаем 2 уравнение
(x - 2)(x - 2) = 1
(x - 2)^2 - 1 = 0
(x - 2 - 1)(x - 2 + 1) = 0
(x - 3)(x - 1) = 0
x1 = 3; y1 = 0
x2 = 1; y2 = -2
ответ: (3; 0); (1; -2)
1. Натуральные 100; 21; 10 (натуральные - это числа, которые возникают при счете предметов.)
Целые 100; 21; 0 ; 10; - 15; -24; (целые - это натуральные, им противоположные и нуль.)
Рациональные -3,2 ; 100; - 14,5; 21; 0; 10; - 15; 1,2333 ...=1.2(3) ; -2,121121112 т.к. можем представить в виде р/q, где р- целое, q- натуральное.
Иррациональные 5, 1313111...; 0,1010010001...; (т.к. иррациональные числа - это числа, которые в десятичной записи представляют собой бесконечные непериодические десятичные дроби).
2.а) каждое натуральное число является целым - да.
б) каждое число является натуральным. - нет.
в) каждое число является рациональным - нет.
г) каждое рациональное число является действительным - да.
д) каждое действительное число является рациональным - нет.
е) каждое иррациональное число является действительным - да.
ж) каждое действительное число является иррациональным - нет.
Задание 3.
Сравните числа. а) 7,653>7,563
б) 1,(56) > 1,56
в) - 4,(45) < -4,45
г) 1,(34) <1,345
Задание 4:
Число 7,15 г) рациональное, т.к. 7,15=715/100
Число - 35. б) целое
2x⁴-6x²+2,5=0
Робимо заміну x^2=t
2t^2-6t+2,5=0
D=6^2-4*2*2,5=36-20=16
t1=(6-4)/(2*2) = 1/2
t2=(6+4)/(2*2) = 2,5
x^2=1/2 x^2=2,5
x1= 1/4 x3=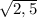
x2= -1/4 x4= -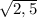
Ну в цілому, якщо додати всі корені, то вийде 0?