Сумма первых n членов геометрической прогрессии:
Распишем сумму первых пяти членов и сумму первых десяти членов:
Разделим второе равенство на первое:
Решим уравнение относительно . Так как сумма коэффициентов равна 0, то:
Первый случай c не реализуется, так как в этом случае сумма первых десяти членов была бы в 2 раза больше, чем сумма первых пяти членов.
Значит, .
Выразим из первого условия выражение для дроби:
Запишем выражение для искомой суммы:
Находим сумму:
ответ: 64540557
Сумма первых n членов геометрической прогрессии:
Распишем сумму первых пяти членов и сумму первых десяти членов:
Разделим второе равенство на первое:
Решим уравнение относительно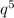 . Так как сумма коэффициентов равна 0, то:
. Так как сумма коэффициентов равна 0, то:
Первый случай c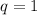 не реализуется, так как в этом случае сумма первых десяти членов была бы в 2 раза больше, чем сумма первых пяти членов.
не реализуется, так как в этом случае сумма первых десяти членов была бы в 2 раза больше, чем сумма первых пяти членов.
Значит,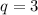 .
.
Выразим из первого условия выражение для дроби:
Запишем выражение для искомой суммы:
Находим сумму:
ответ: 64540557