Нет решения
Объяснение:
d = b² - 4ac = 9 - 16 = -7, но так как корня из отрицательного числа не существует у уравнения нет решения.
,
, a 
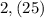
целая часть. У нас она равна 2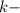
- количество цифр в периоде. У нас их 2
количество цифр до периода. У нас их 0
все цифры, включая период, в виде натурального числа. У нас это 25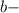
все цифры без периода в виде натурального числа. Их нет.
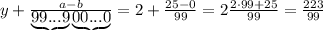
подставляется количество 9, а под 
-количество нулей. У нас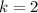 
, значит пишем две цифры 9, а 
, значит, нулей не пишем вообще. Между 
не стоит знак умножения
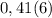
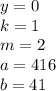
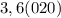
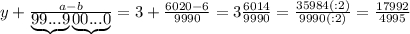
97,5
Объяснение:
Данная задача решаема через систему уравнения:
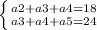
Решим эту систему при метода вычитания:
a3+a4=18-a2
a3+a4+24-a5
24-a5=18-a2
6-a5+a2=0
a5-a2=6 - данное выражение показывает нам разницу между членами прогресcии через a3 и a4
Разница между ближайшими членами d = 1,5 ,потому-что согласно a5-a2=6
Теперь есть формула:
a2=a1+d => d=1,5 => a2=a1+d ,тогда подставим в первое уравнение системы:
a1+1,5+a3+a4=18
Но при этом а3=a1+3 и а4=а1+4,5
Тогда:
a1+1,5+a1+3+а1+4,5=18
3*a1+9=18
a1=3
Находим все члены и их сумма равна:
3+4,5+6+7,5+9+10,5+12+13,5+15+16,5=97,5
ответ: 97,5
(В решении или в вычислениях могу ошибаться!)
.....................