Пусть 
(км/ч) - первоначальная скорость мотоциклиста.
Тогда время, за которое он преодолел путь в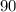 
километров, равно 
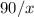часов.
Но, с другой стороны, сумма трех других отрезков времени равна тому же промежутку времени (по условию). Это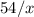 
часов, 
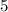минут или же 
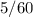часа = 
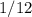часа. И последний промежуток, 
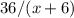часов (
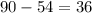километров со скоростью 
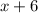км/ч).
Теперь, конечно, будем решать уравнение:
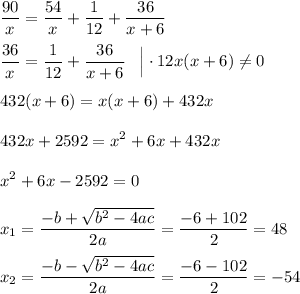
Получилось два корня. Второй доверия не внушает из-за своей отрицательности, так что возьмем исключительно первый.
Первоначальная скорость мотоциклиста -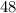 
км/ч.
Задача решена!
ответ: 48 км / ч .
1) a) 2x²-8;
недопустимых значений переменной x не существует, т.к 2x²-8 - не знаменатель дроби, нет корня и т.д => x ∈ R
б) дробь имеет смысл, когда знаменатель не равен нулю: x-2≠0
x≠2
x∈(-∞; 2) ∪ (2; +∞)
в) x+3≠0
x≠-3
x ∈ (-∞; -3) ∪ (-3; +∞)
2) a) дробь имеет смысл, когда знаменатель не равен нулю
y²-4≠0
(y-2)(y+2)≠0
y≠-2
y≠2
y ∈ (-∞; -2) ∪ (-2; 2) ∪ (2; +∞)
б) дробь имеет смысл, когда знаменатель не равен нулю
y²+1≠0
y²≠-1 - нет действительных корней
y∈R
в) дроби имеют смысл, когда знаменатели не равны нулю
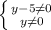
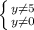
y ∈ (-∞; 0) ∪ (0; 5) ∪ (5; +∞)
Объяснение:
1. с) 4 см.
2. d) 14 см.
3. в) 8 см.
Объяснение:
". Основание равнобедренного треугольника равно 10 см., а боковая сторона 8 см. чему равна длина отрезка, соединяющего середины основания и боковой стороны?"
***
АВС - треугольник. АВ=ВС=8 см. MN - средняя линия треугольника MN║AB и равно его половине МН=АВ/2=8/2=4 см.
***
"В квадрате с диагональю 7 см последовательно соединили отрезками середины сторон. Найдите периметр образованного четырехугольника."
***
ABCD - квадрат. АС=7 см - диагональ квадрата.
Соединили середины сторон квадрата. Получили квадрат A1B1C1D1? стороны которого являются средними линиями диагоналей квадрата и равны его половине.
A1B1=B1C1=C1D1=A1D1=AC/2=7/2=3.5 см .
Р=4А1В1=4*3,5=14 см.
***
3. Средняя линия треугольника параллельна основанию и равна его половине.
АВС - равносторонний треугольник. MN =4 см - средняя линия. MN║AC. MN=AC/2. AC=2*MN=8 см .