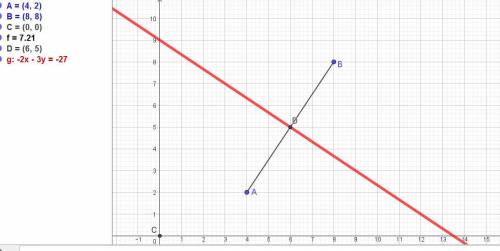
Прямая,все точки которой находятся на равных расстояниях от точек A(4;2) и B(8;8), это перпендикуляр к середине отрезка АВ.
Уравнение АВ: (х - 4)/(8 - 4) =(у - 2)/(8 - 2).
(х - 4)/4 =(у - 2)/6) или (х - 4)/2 =(у - 2)/3.
Или в общем виде Ах + Ву + С = 0.
3х - 12 = 2у - 8,
3х - 2у - 4 = 0. Здесь А = 3, В = -2.
Перпендикулярная прямая имеет вид -Вх + Ау + С1 = 0.
Для определения коэффициента С1 надо подставить координаты точки, принадлежащей этой прямой.
Такая точка - середина АВ (точка Д).
Д = (1/2)(A(4;2) + B(8;8))/2 = (6; 5). Подставляем:
2*6 + 3*5 + С1 = 0,
С1 = -12 - 15 = -27.
ответ: уравнение прямой, все точки которой находятся на равных расстояниях от точек A(4;2) и B(8;8), это 2х + 3у - 27 = 0.
cos 4x = 1 - 2 sin^2 2x
2.Свернем 26 sin x cos x по формуле 2-го угла для sin и получим
13 sin 2x
3.Теперь наше уравнение выглядит как
13 sin 2x - (1 - 2 sin^2 2x) + 7 = 13 sin 2x - 1 + 2 sin^2 2x + 7 = 2 sin^2 2x + 13 sin 2x + 6 = 0
Делаем замену t = sin 2x t^2 = sin^2 2x
4.Получаем квадратное уравнение
2t^2 + 13t + 6 = 0
Находим корни
t1 = -0.5
t2 = 6
так как sin 2x может быть только -0.5 считаем корень для этого значения
sin 2x = -1/2
2x = (-1^n) * arcsin(-1/2) + pin, n∈Z
2x = (-1^n+1) * arcsin(1/2) + pin, n∈Z - здесь мы убрали минус из под arcsin
ответ : x = (-1^n+1) * pi/6 + pin/2, n∈Z
Надеюсь объяснил подробно!)