


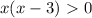
 ∈
∈ 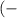 ∞
∞  ∪
∪ 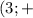 ∞
∞ 

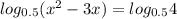
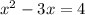
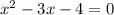
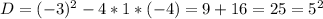
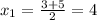
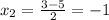



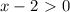
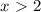
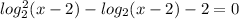

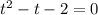

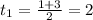

 или
или 
 или
или 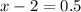
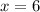 или
или 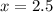

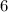
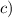
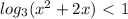

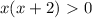
 ∈
∈ 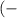 ∞
∞  ∪
∪ 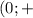 ∞
∞ 

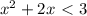


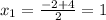

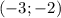 ∪
∪ 
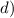
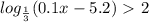







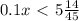



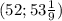
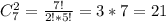 , всего выбрать два черных шара:
, всего выбрать два черных шара: 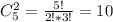 . Вероятность:
. Вероятность: 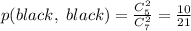
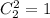
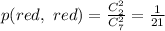
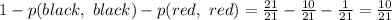
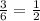 . На второй подойдут 3, 4, 5, 6. Вероятность выпадения
. На второй подойдут 3, 4, 5, 6. Вероятность выпадения 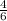 . Т.к. события независимые, то вероятности перемножаем.
. Т.к. события независимые, то вероятности перемножаем. 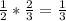 .
.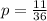
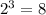 вариантов: ннн, ппп, нпп, ннп, пнп, ппн, пнн, пнп.
вариантов: ннн, ппп, нпп, ннп, пнп, ппн, пнн, пнп.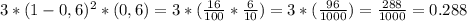
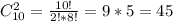
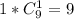 .
.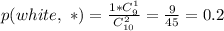
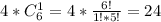 (т.к. не чёрных у нас 6, 5 красных и 1 белый.)
(т.к. не чёрных у нас 6, 5 красных и 1 белый.)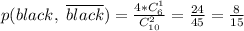
sixty five years later she had been married for 6th and had been living with the mother in a hospital in the late afternoon of her life and her family had to see the world of her life in a few weeks of her childhood