1. (6;-1) 2. (5; -1) 3. (-3;13) 4.(-3.5;-1) 5. (-1;2).
Объяснение:
1. Сложим 2 уравнения. y сократиться и получим:
2x=12
x=6.
Подставим полученный x=6 в любое уравнение системы (например в первое, получим уравнение относительно y , которое решим:
6+y=5;
y=5-6;
y= -1.
2. Домножим обе части первого уравнения на 5. Получим систему:
5x+5y=20;
3x-5y=20.
Сложим два уравнения, 5y и -5y сократятся дав в сумме 0.
получим уравнение относительно x:
8x=40;
x=5.
Подставляем x=5 например в первое уравнение:
5+y=4;
y=4-5;
y=-1.
3. 
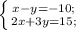
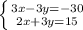
Складываем два уравнения:
5x=-15
x=-3
3-y=-10
-y=-10-3
y=10+3
y=13.
4. Первое ур-е умножим обе части на 3 а второе ур-е умножим обе части на -2.
Получим новую систему:
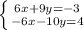
9y-10y=-3+4
-y=1
y=-1.
Подставляем в первое уравнение исходной системы y=2.
2x+3*2=-1
2x+6=-1
2x=-1-6
2x=-7
x=-3.5.
5. 
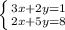
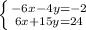
-4y+15y=-2+24;
y=2.
3x+2*2=1;
3x+4=1;
3x=1-4;
3x=-3;
x=-1.
Задача: Моторний човен пройшов 8 км за течією річки і 5 км проти течії, затративши на весь шлях 1 год. Знайти швидкість човна у стоячій воді, якщо швидкість течії річки дорівнює 3 км/год.
Рішення: Нехай х км/год — швидкість човна в стоячій воді, тоді швидкість човна за течією — х+3 км/год, а проти течії — х-3 км/год. Човен пройшов 8 км за течією 8/(х+3) год, а проти течії — 5/(х-3) год. Весь шлях човен пройшов за 1 год. Складемо і вирішимо рівняння.
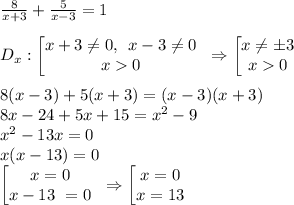
Відповідь: Швидкість човна у стоячій воді дорівню 13 км/год.
y > 0 : (-∞ ;
] ∪ 
+∞)
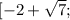y < 0 :![[- 2 - \sqrt{7} ;- 2 + \sqrt{7} ]](/tpl/images/1576/3568/364d1.png)
функция убывает: (-∞ ; -2)
Объяснение:
y = x^2 + 4x - 3
строим график:
минимумы потому что a > 0 и парабола ветвями вверх
х минимум = -b / 2a = -4/2 = -2
y минимум = 4 + 4*(-2) - 3 = 4 - 8 - 3 = -7
y (0) = -3
решим уравнение x^2 + 4x - 3 = 0 и найдем пересечения функции с осьюХ:
x нулевые = -2 +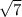
; -2 -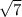 
исследуем график:
функция убывает: (-∞ ; -2)
y > 0 : (-∞ ;
] ∪ 
+∞)
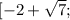y < 0 :![[- 2 - \sqrt{7} ;- 2 + \sqrt{7} ]](/tpl/images/1576/3568/364d1.png)