Приклад:
Розв'язати систему рівнянь: {x−2y=3,5x+y=4.
1) З першого рівняння системи виражаємо змінну x через змінну y.
Отримуємо: x−2y=3,x=3+2y;
2) Підставимо отриманий вираз замість змінної x у друге рівняння системи:
5⋅x+y=4,5⋅(3+2y)+y=4;
3) Розв'яжемо утворене рівняння з однією змінною, знайдемо y:
5⋅(3+2y)+y=4,15+10y+y=4,10y+y=4−15,11y=−11,|:11y=−1¯¯¯¯¯¯¯¯¯¯¯.
4) Знайдемо відповідне значення змінної x, підставивши значення змінної y, у вираз знайдений на першому кроці:
x=3+2⋅y,x=3+2⋅(−1),x=3−2,x=1¯¯¯¯¯¯¯¯.
5) Відповідь: (1;−1) .
Объяснение:
это решить линейные уравнения без черчежей
16%
Объяснение:
допустим исходная стоимость товара х
x* 3/5 идет с наценкой 5%. то есть этот товар стал стоить на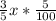 дороже. то есть цена этого товара стала
дороже. то есть цена этого товара стала 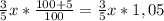
Осталость 2/5 товара. Половина его, то есть 1/5 продавалась с наценкой 4%, то есть она стоила 1,04x*1/5
Оставшиеся 1/5 товара продавалист с неизвестной наценкой y%, она стоила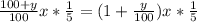
В итоге товар стоил
1,05*x*3/5 + 1,04*x*1/5 + (1+y/100))*x*1/5= (1,05*3+1,04 +(1+y/100)x/5
с другой сторны общая наценка оказалась 7%, то есть товар стал стоить 1,07х
Получаем уравнение
(1,05*3+1,04 +(1+y/100))x/5=1,07х
Сокращаеи на х
(1,05*3+1,04 +(1+y/100))/5=1,07
1,05*3+1,04 +(1+y/100)=1,07*5
3,15+1,04 +1 +y/100=5,35
5,19 +y/100=5,35
y/100=0,16
y=16