ну неравенств очень много не скажешь что у низ есть какой та определенный алгоритм
Например линейные
2x<5
x<5/2
квадратичные
x^2+2x<0
x(x+2)<0
x<0
x<-2
то есть твоя цель это найти при каких отрезков , то есть значений которых ты найдешь будут являться решениями!
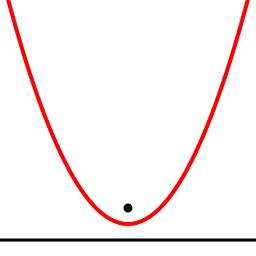
Парабола y=x^2 функцией графика являеться парабола
парабола нужна Допустим в прикладной сфере математики на наибольшее значений нахождение очень полезна то есть ты как бы решаешь какую ту задачу сводишь ее к квадратному, если она сводиться конечно, находишь наибольшее значение
так как она находиться в самом начале параболы а формула известна Ymax=-b/2a
A1 = -7
A2 = A1+d=-4
A3 = A2+d=A1 + 2d = -1
An = A(n-1)+d = A1 + (n-1)*d
S = 430
S= (A1+An)*n/2
(A1 + A1 + (n-1)*d)*n/2 = 430
(A1 + A1 + (n-1)*d)*n = 860
A1*n + A1*n + d*n^2 - d = 860
3n^2-17n-860 =0
D=(17)^2 + 4*3*860 = 10609
n1 = (17-103)/6 = -14.333 не удавлетворяет, числа должныбыть положительные и целые
n1 = (17+103)/6 = 20
Проверяем
A20=A1+(20-1)*d=-7+19*3=50
S20=(A1+A20)*n/2=(-7+50)*20/2=430 что и требовалось найти
ответ: Число элементов арифметической прогрессии равно 20