1) 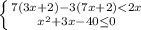
7(3x+2)-3(7x+2)<2x
21x+14-21x-6<2x
8<2x
-2x<-8
x>4
x²+3x-40≤0
x²+3x-40=(x-5)(x+8)
D=13²
x1=5
x2=-8
(x-5)(x+8)≤0
5 -8
x∈[-8;5]
После объединения в один чертёж:
ответ: x∈(4;5]
2) 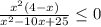
x²-10x+25≠0
D=0
x≠5
x²-10x+25=(x-5)²
x²(4-x)≤0
-x²(x-4)≤0
⇒ -x²(x-4)*(x-5)²≤0
-x²=0
x=0(знак на чертеже дублируется)
x-4=0
x=4
(x-5)²=0
x=5(знак дублируется и 5 выкалывается)
ответ: x∈[4;5)∪(5;∞)
3) 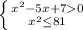
x²-5x+7>0
x²-5x+7
D=25-28=-3
⇒x>0 при любых x
Дополнительно: После D=-x - не всегда неравенство имеет решение - надо смотреть по графику (в вашем случаи - при любых x)
x²≤81
x²-81≤0
(x-9)(x+9)≤0
9;-9
ответ: x∈[-9;9]
1)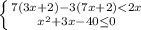
7(3x+2)-3(7x+2)<2x
21x+14-21x-6<2x
8<2x
-2x<-8
x>4
x²+3x-40≤0
x²+3x-40=(x-5)(x+8)
D=13²
x1=5
x2=-8
(x-5)(x+8)≤0
5 -8
x∈[-8;5]
После объединения в один чертёж:
ответ: x∈(4;5]
2)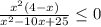
x²-10x+25≠0
D=0
x≠5
x²-10x+25=(x-5)²
x²(4-x)≤0
-x²(x-4)≤0
⇒ -x²(x-4)*(x-5)²≤0
-x²=0
x=0(знак на чертеже дублируется)
x-4=0
x=4
(x-5)²=0
x=5(знак дублируется и 5 выкалывается)
ответ: x∈[4;5)∪(5;∞)
3)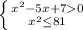
x²-5x+7>0
x²-5x+7
D=25-28=-3
⇒x>0 при любых x
Дополнительно: После D=-x - не всегда неравенство имеет решение - надо смотреть по графику (в вашем случаи - при любых x)
x²≤81
x²-81≤0
(x-9)(x+9)≤0
9;-9
ответ: x∈[-9;9]