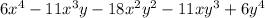 2. Найти НОД многочленов
2. Найти НОД многочленов 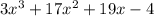 и
и 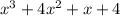
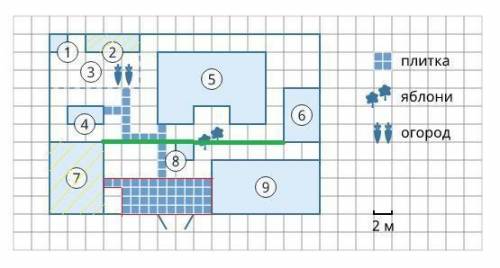
1) 5коробок 2) 60 м² 3) 20 м
Объяснение:
1) По рисунку видно, что 1 плитка 0,5*0,5 клетки, или с учетом масштаба:
0,5*0,5*2*2=1 м²
По схеме видно, что дорожка занимает 5*2 клеток и еще 0,5*1 клетку. Рассчитаем площадь плитки с учетом масштаба:
5*2*2*2+0,5*1*2*2=42 м² занимает площадь плитки от коровника к курятнику
42:1=42 плитки
42:10=4,2 коробки округляем в большую сторону до целого 5 коробок
2) Размер теплицы в клетках: 3*1
Размер коровника в клетках: 3*4
Площадь коровника и теплицы с учетом масштаба:
3*1*2*2+3*4*2*2=60 м²
3) Расстояние между двумя ближайшими точками - это расстояние от правого верхнего угла коровника до левого нижнего угла коровника.
Это 10 клеток или 10*2=20 м
Умножаем на -1, при этом меняется знак неравенства
x(x - 7) < 0
По методу интервалов x ∈ (0; 7)
2) x^2*(3 - x)(x + 1) <= 0
Умножаем на -1, при этом меняется знак неравенства
x^2*(x - 3)(x + 1) >= 0
x^2 > 0 при любом x =/= 0. Поэтому x = 0 - это решение.
Делим на x^2
(x - 3)(x + 1) >= 0
По методу интервалов x ∈ (-oo; -1] U [3; +oo)
Добавим решение x=0 и получим:
x ∈ (-oo; -1] U [0] U [3; +oo)
3) 3x^2 - 7x + 2 < 0
D = 7^2 - 4*3*2 = 49 - 24 = 25 = 5^2
x1 = (7 - 5)/6 = 2/6 = 1/3; x2 = (7 + 5)/6 = 12/6 = 2
По методу интервалов x ∈ (1/3; 2)