48 квадратных сантиметров
Объяснение:
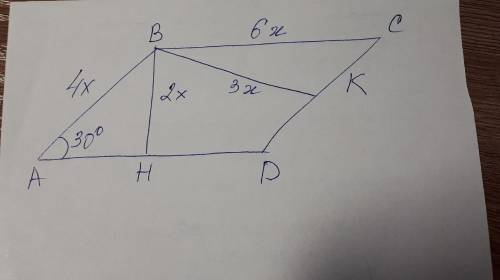
1) Примем одну высоту параллелограмма за 2х (на рисунке это сторона BH), тогда вторую высоту примем за 3х (на рисунке это сторона BK).
2) Поскольку катет против угла в 30° равен половине гипотенузы, то из треугольника АВН получаем, что гипотенуза АВ = 4х.
3) Далее рассмотрим треугольник ВСК. Получаем, что сторона ВС= 6х
4) Затем вычислим периметр параллелограмма: (4х+6х)*2=40 сантиметров
5) 20х=40, откуда х=2
6) Таким образом, можно сделать вывод, что одна сторона 4х=4·2=8 см.
7) Высота проведенная к этой стороне 3х=3·2=6 см
8) Таким образом получаем, что площадь параллелограмма равна 8*6=48 квадратных сантиметров
Сразу пишу, что получится через равно
а) =2(х-у)+(х-у)= (2+1)(х-у)=3(х-у)
б) =b(a+2c)+(a+2c)=(b+1)(a+2c)
в) =(3х+2а)-с(3х+2а)=(1-с)(3х+2а)
г) =3(х+у)+а(х+у)=(3+а)(х+у)
д) =5(а-b)-c(a-b)=(5-c)(a-b)
е) =а(с-2d)-x(c-2d)=(a-x)(c-2d)
ё) =2d(2a+3x)-3c(2a+3x)=(2d-3c)(2a+3x)
ж) =x(x^2+1)+y(x^2+1)=(x+y)(x^2+1)
з) =a(a-b)+c(a-b)=(a+c)(a-b)
и) =a^2(a+b)+x(a+b)=(a^2+x)(a+b)
й) =a^5(a+1)-a^3(a+1)=(a^5-a^3)(a+1)