Станадартный вид - это a * 10 в степени n, где 1<n<10
35,7*10 в степени -8 = 3,57*10 в степени -7
В решении.
Объяснение:
Дана функция у=√х:
а) График которой проходит через точку с координатами А(а; 9). Найдите значение а.
Нужно в уравнение подставить известные значения х и у (координаты точки А):
9 = √а
(9)² = (√а)²
81 = а
а=81;
b) Если х∈[0; 8], то какие значения будет принимать данная функция?
у= √х
у=√0=0;
у=√8=√8;
При х∈ [0; 8] у∈ [0; √8].
с) y∈ [4; 121]. Найдите значение аргумента.
4 = √х
(4)² = (√х)²
х=16;
121 = √х
(121)² = (√х)²
х=14641;
При х∈ [16; 14641] y∈ [4; 121].
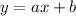- a угловой коэффициент,b точка пересечения прямой с осью у.
, следовательно, данные прямые пересекают ось у в начале координат.
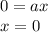
- область определения.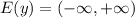
- область значений.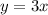
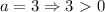, следовательно, данная функция всегда возрастает.
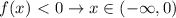
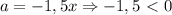следовательно, данная функция всегда убывает.![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)
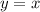
, следовательно, данная функция всегда возрастает.
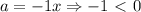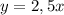
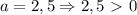следовательно, данная функция всегда убывает.
, следовательно, данная функция всегда возрастает.
следовательно, данная функция всегда убывает.
a = 35.7 * 10 ^ - 8 = 35.7 * (1/100000000) = 0,000000357