(у^3-y)+(-3y^2-3)=0
y(y^2-1)-3(y^2-1)=0
(y^2-1)(y-3)=0
y=1 ,y=-1, y=3
ответ: 2 км/час.
Объяснение:
Дано. Катер плыл 2,3 ч по течению
и 3,5 ч против течения.
Всего он проплыл 133,9 км.
Найдите скорость течения, если
собственная скорость катера 23,5 км/ч.
Решение.
Обозначим скорость течения через х км/час.
Тогда скорость катера по течению будет 23,5+х км/час
скорость против течения --- 23,5 - х км/час.
S=vt.
Путь по течению равен
S1= (23,5+х)2.3 = 54.05 +2.3x км.
Путь против течения равен
S2=(23.5-x)3.5 = 82.25-3.5x км.
Весь путь равен 133,9 км.
Составим уравнение:
54,05+2,3х + 82,25-3,5х = 133,9;
2,3х-3,5х = 133,9-54,05-82,25;
-1,2х=-2,4;
х=2 км/час - скорость течения реки.
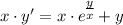
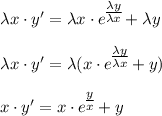
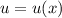с замены:
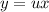, тогда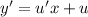 
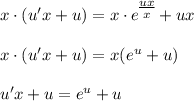
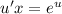
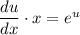- уравнение с разделяющимися переменными.
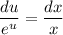- уравнение с разделёнными переменными.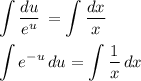
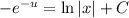- общий интеграл новой функции.
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: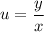 
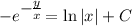- общий интеграл исходного уравнения.
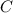. Подставим в общий интеграл начальное условие: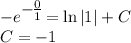
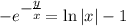- частный интеграл, также является решением данного дифференциального уравнения.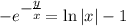
(у^3-y)+(-3y^2-3)=0
y(y^2-1)-3(y^2-1)=0
(y^2-1)(y-3)=0
y=1 ,y=-1, y=3