|x + 2|(x² – a²) > 0
1) a ≤ –2: x ∈ (–∞; a) ∪ (–a; +∞)
2) –2 < a < 0: x ∈ (–∞; a) ∪ (–a; +∞) \ {–2}
3) a = 0: x ∈ (–∞; +∞) \ {–2; 0}
4) 0 < a < 2: x ∈ (–∞; –a) ∪ (a; +∞) \ {–2}
5) a ≥ 2: x ∈ (–∞; –a) ∪ (a; +∞)
Объяснение:
Выражение |x + 2|(x² – a²) -- может менять знак только в точках, являющихся корнями уравнения |x + 2|(x² – a²) = 0, то есть корни делят числовую прямую на интервалы, в пределах которых знак сохраняется.
Для решения неравенства |x + 2|(x² – a²) > 0 необходимо нанести корни на числовую прямую и пометить те интервалы, на которых выражение |x + 2|(x² – a²) является положительным. Сами корни не будут входить в ответ, поскольку неравенство строгое.
Корнями являются значения x₁ = –2, x₂ = –a, x₃ = a. Существует несколько возможных вариантов расположения этих корней на числовой прямой, поэтому необходимо рассмотреть их все по отдельности (см. рисунок).
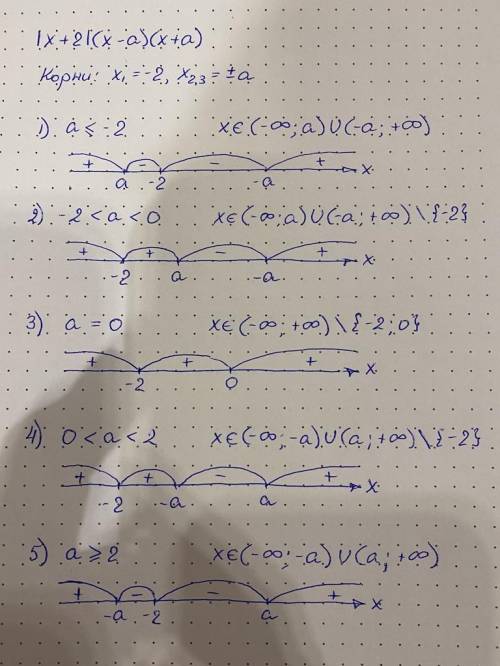
х² -2х*2 +4 - 4 +3 = 0
(х-2)² = 1
х -2 = 1 или х -2 = -1
х = 3 х = 1
2)x^2 - 6x+5=0
х² -2х*3 +9 -9 +5 = 0
(х-3) = 4
х-3 = 2 или х -3 = -
х = 5 х = -1
3)x^2+8x-20=0
х² +2х*4 +16 -16 -20 = 0
(х+4)² = 4
х +4 = 2 или х +4= -2
х = -2 х = -6
4)x^2+12x+32=0
х² +2х*6 +36 -36 +32 = 0
(х +6)² = 4
х +6 = 2 или х +6 = -2
х = -4 х = -8
5)x^2-2x-15=0
х² -2х*1 +1 -1 -15 = 0
(х-1)² = 16
х-1 = 4 или х-1 = -4
х = 5 х = -3
6)X^2-4x-45=0
х² -2х *2 +4 -4 -45 =0
(х-2)² = 49
х-2 = 7 или х -2 = -7
х = 9 х = -5