
В решении.
Объяснение:
Знайдіть усі точки графіка функції y=x2−5x+3 , у яких абсциса та ордината є протилежними числами.
Найдите все точки графика функции y=x² - 5x + 3 , в которых абсцисса и ордината являются противоположными числами.
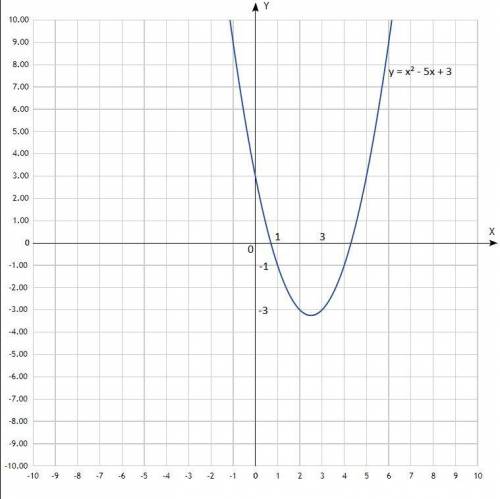
Дана функция у = х² - 5х + 3.
Построить график. График - парабола со смещённым центром, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3 4 5 6 7 8
у 27 17 9 3 -1 -3 -3 -1 3 9 17 27
Согласно таблицы и графика существует две точки с указанными значениями х и у:
координаты: (1; -1); (3; -3).
Находим точки, в которых неравенство равно нулю:
x-1=0 x=1
x+5=0 x=-5
Наносим на прямую (-∞;+∞) эти точки:
-∞-51+∞
Получаем три диапазона: (-∞;-5) (-5;1) (1;+∞)
Для того, чтобы определить знак диапазона достаточно подставить хотя бы одно число из этого диапазона:
(-∞;-5) Например, подставим число -7: (-7-1)(-7+5)=-8*(-2)=16>0 ⇒ +
(-5;1) Подставим число этого диапазона 0: (0-1)(0+5)=-1*5=-5<0 ⇒ -
(1;+∞) Подставим 2: (2-1)(2+5)=1*7=7>0 ⇒ +
-∞+-5-1++∞ ⇒
x∈(-∞;-5)U(1;+∞).