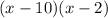формула электроемкости конденсатора
определение
конденсатором называют совокупность двух проводников, имеющие одинаковые по модулю и противоположные по знаку заряды.
проводники у конденсатора называют обкладками конденсатора.
обкладки должны иметь такую форму и
быть расположены так относительно друг друга, что поле, которое создается данной системой, было максимально в ограниченной области пространства, между обкладками.
назначение конденсатора в том, чтобы накапливать и отдавать в электрической цепи заряд.
основной
характеристикой конденсатора является электрическая емкость (c). электрическая емкость конденсатора – это взаимная емкость принадлежащих ему обкладок:
\[c=\frac{q}{{\varphi }_1-{\varphi }_2}=\frac{q}{u} \qquad(1)\]
q – величина заряда на обкладке;
{\varphi }_1-{\varphi }_2 – разность потенциалов между обкладками.
электрическая ёмкость конденсатора зависит от диэлектрической проницаемости диэлектрика, который заполняет пространство между его обкладками. если пространство между обкладками одного конденсатора заполнено диэлектриком
с проницаемостью равной \varepsilon, а у второго конденсатора воздух между пластинами, то емкость конденсатора с диэлектриком (c) в \varepsilon раз больше, чем емкость воздушного конденсатора (c_0):
\[c=\varepsilon c_0 \qquad(2)\]
треугольник задается своими тремя вершинами.
случай 1. пусть одна из вершин треугольника лежит на первой прямой, у которой 10 точек, а две другие - на второй прямой, у которой 6 точек.
первую вершину можно выбрать способами, а две другие - способами. по правилу
произведения, всего треугольников
случай 2. пусть одна вершина теперь лежит на второй прямой, а две другие - на первой прямой. тогда первую вершину можно взять способами, а две другие - способами. по правилу произведения, всего таких треугольников -
6*45=270
итак, искомое количество треугольников равно
Разложим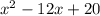
на множители с группировки.
Разложи выражение на множители путем группировки. Сначала выражение необходимо переписать в следующем виде: x^2 +ax+bx+20. Чтобы найти a и b, настрой систему для решения.
Поскольку ab положительное, a и b имеют одинаковый знак. Так как a+b отрицательный, a и b являются отрицательными. Перечисли все такие пары, содержащие 20 продукта.
Вычисли сумму для каждой пары.
−1−20=−21
−2−10=−12
−4−5=−9
Решение — это пара значений, сумма которых равна −12.
Перепишите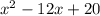
как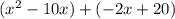 
Вынесите за скобки общий член x−10, используя свойство дистрибутивности.
Получим