х(х-5)-29>5(4-x)
х^2-5x-29>20-5x
х^2-5x-29-20+5x>0
х^2-49>0
(х-7)(х+7)>0
x[(-бесконечности,-7 )и(7,+бесконечности)
х²-4х-45=0
D=16-4*1*(-45)=196
x1=(4-16)\2=-6
x2=(4+16)\2=10
Решить уравнение - значит найти все такие значения переменной(-ых), при которых уравнение обращается в верное числовое равенство. Эти значения - корни уравнения.
Основными свойствами уравнения являются следующие два:
1) Если к обеим частям уравнения прибавить (или отнять) одно и тоже число (переменную, многочлен и т.д.), то полученное уравнение будет равносильно данному. Например, 3-у=27. Если мы из обеих частей уравнения вычтем 3, то получим следующее: -у=24. Данное уравнение равносильно исходному.
2) Если обе части уравнения умножить (или разделить на одно и то же число (многочлен, переменную и т.д.)), то полученное уравнение будет равносильно данному. Например, 3х=6. Разделив обе части уравнения на 3, получим следующее: х=2. Эти уравнения равносильны.
В обоих случаях стоит внимательно следить за составляющими уравнения. Если вдруг это дробно-рациональное уравнение, то знаменатель не должен стать нулём ни при каких вычетах и домножениях дроби.
Равносильные уравнения - уравнения, имеющие одинаковое множество корней. Например, х²=4 и (х-2)(х+2)=0 - равносильные уравнения.
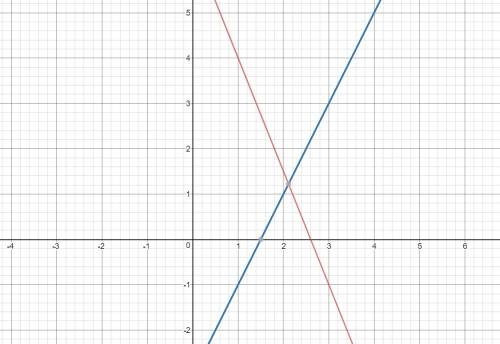
Линейное уравнение - уравнение вида (если оно полное, с двумя переменными) ax+by+c=0, где или а, или b ≠0, графиком которого служит прямая. Решение - всякая пара чисел, которая обращает многочлен ax+by+с в нуль.
+ - +
________________ -7 ______________ 7 _________________
2. Выражение х²-4х-45 имеет смысл при любых значениях х.