Объяснение:
Часть 1
1. Параллелограммом называется четырехугольник, у которого противолежащие стороны ...
1.параллельны
2.равны
3.пересекаются
4.перпендикулярны
2. Дайте название следующему утверждению: в параллелограмме противоположные стороны равны. 1.определение параллелограмма
2.признак параллелограмма
3.аксиома
4.свойство параллелограмма
3)В параллелограмме ABCD углу А противоположным будет угол ?
1. В
2. С
3. D
4. В параллелограмме нет противоположных углов
4. Какова сумма любых двух соседних углов в параллелограмме?
1) 180°
2) бывает разной
3) 270°
4) 90°
5. В четырехугольнике два противоположных угла равны. Является ли он параллелограммом?
1) не является
2) не обязательно
3) такая ситуация невозможна
4) является
6. Один из углов параллелограмма равен 35°. Чему равны остальные его углы?
1) 145°, 35°, 145°;
2) 55°, 125°, 5°;
3) 35°, 145°, 50.
Сумма двух соседних углов равна 180°, значит второй угол : 180 - 35= 145°. Противоположные углы в параллелограмме равны , значит оставшиеся углы : 145°;35°; 145°
7. Биссектрисы соседних углов параллелограмма:
1) перпендикулярны
2) параллельны
3) пересекаются и точкой пересечения делятся пополам
4) невозможно их провести
8. Продолжите: Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.
9. Вставьте пропущенное слово: В параллелограмме противоположные стороны равны
10.Вставьте пропущенные слова: Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм
Часть 2 (задачи)
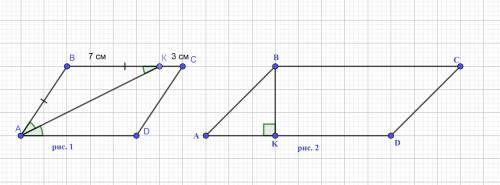
1.В параллелограмме АВСD биссектриса угла А пересекает сторону ВС в точке К так, что ВК = 7 см, КС = 3 см. Чему равен периметр параллелограмма?
Биссектриса угла в параллелограмме отсекает от него
равнобедренный треугольник, поэтому Δ АВК равнобедренный, значит АВ=ВК= 7 см
Сторона ВС=ВК+ КС= 7+3=10 см
Р=2*(АВ+ВС) =2*(10+7)=2*17 =34 см
ответ : Р= 34 см
( рис. 1 во вложении)
2. Из вершины В параллелограмма ABCD с острым углом А проведен перпендикуляр BK к прямой AD; ВК =1/2АВ. Найдите углы С и D
Рассмотрим Δ ABK. ( рис. 2) Он прямоугольный (∠ ВКА = 90°).
По условию BK = 1/ AB. А поскольку AB – гипотенуза Δ АВК ., то ∠ А = 30 ° (катет, лежащий против угла в 30 ° равен половине гипотенузы).
Поскольку в параллелограмме противолежащие углы равны, то
∠ С = 30 °
Теперь найдем ∠ D. В параллелограмме сумма внутренних углов равна 360 ° , значит
∠ D = ∠B = (360° - 2*30°):2= 150°.
ответ: C = 30 градусов, D = 150 градусов
( рис.2 во вложении)
1. Даны вершины треугольника А(10,6),В(-1,-2),С(-4,7).
1) Расчет длин сторон
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √185 ≈ 13,6014705.
BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √90 ≈ 9,486833.
AC (в) = √((Хc-Хa)²+(Ус-Уa)²) = √197 ≈ 14,035669.
Уравнения сторон
АВ : Х-Ха = У-Уа
Хв-Ха Ув-Уа
у = 0,727272727 х - 1,272727273,
-8Х + 11У + 14 = 0.
ВС : Х-Хв = У-Ув
Хс-Хв Ус-Ув
у = -3х - 5,
3Х + 1У + 5 = 0.
АС : Х-Ха = У-Уа
Хс-Ха Ус-Уа
у = -0,071428571 х + 6,714285714,
1Х + 14У - 94 = 0.
2) Вектор АВ = В(1; 4) - А(1;-2) = (0; 6), модуль равен 6.
Вектор АС = С(-4; 1) - А(1;-2) = (-5; 3), модуль равен √(25+9) =√34.
cos A = (0*(-5)+6*3)/(6*√34) = 18/(6√34) ≈ 0,764775345
Угол А = 0,700103751 радиан или 40,11299017 градусов.
3) Площадь треугольника ABC:
S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 61,5
.
Периметр Р = 37,12397
.
2. Даны вершины четырехугольника А(1,-2),В(1,4), С(-4,1), D(-5,-6).
Расчет длин сторон
АВ = √((Хв-Ха)²+(Ув-Уа)²) = √36 = 6.
BC = √((Хc-Хв)²+(Ус-Ув)²) = √34 ≈ 5,830952.
СД = √((Хд-Хс)²+(Уд-Ус)²) = √50 ≈ 7,071068.
AД = √((Хд-Хa)²+(Уд-Уa)²) = √52 ≈ 7,2111026.
Периметр Р = 26,113122.